Wprowadzenie
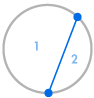
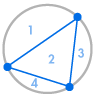
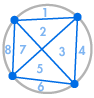
Wyobraźmy sobie, że umieszczamy kilka punktów na obwodzie koła i łączymy każdy punkt ze sobą. W ten sposób dzielimy okrąg na wiele różnych regionów, a w każdym przypadku możemy policzyć ich liczbę. Poniższe diagramy pokazują, ile jest regionów dla kilku różnych liczb punktów na obwodzie. Musimy się upewnić, że na każdym przecięciu wewnątrz okręgu spotykają się tylko dwie linie, a nie trzy lub więcej.
 |
 |
 |
 |
 |
| 1 region | 2 regiony | 4 regiony | 8 regionów | 16 regionów |
Od razu widzimy pewien wzór: liczba regionów jest zawsze dwa razy większa od poprzedniej, tak że otrzymujemy sekwencję 1, 2, 4, 8, 16, … Oznacza to, że przy 6 punktach na obwodzie byłyby 32 regiony, a przy 7 punktach byłyby 64 regiony.
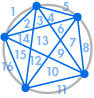
Możemy zdecydować, że jesteśmy zadowoleni z tego wyniku. Liczba regionów jest zawsze dwa razy większa od poprzedniej – w końcu to działało dla pierwszych pięciu przypadków. Albo możemy zdecydować, że powinniśmy sprawdzić jeszcze kilka innych, tak dla pewności:
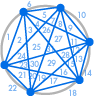 |
 |
| 31 regionów, nie 32 | 57 regionów, nie 64 |
Niestety coś poszło nie tak: 31 może wyglądać na błąd w liczeniu, ale 57 to znacznie mniej niż 64. Sekwencja trwa 99, 163, 256, …, bardzo różni się od tego, co otrzymalibyśmy podwajając poprzednią liczbę.
Ten przykład ilustruje, dlaczego w matematyce nie można po prostu powiedzieć, że obserwacja jest zawsze prawdziwa, tylko dlatego, że działa w kilku przypadkach, które przetestowaliśmy. Zamiast tego musisz wymyślić rygorystyczny logiczny argument, który prowadzi od wyników, które już znasz, do czegoś nowego, co chcesz pokazać, że jest prawdziwe. Taki argument nazywa się dowodem.
Dowody są tym, co odróżnia matematykę od wszystkich innych nauk, ponieważ kiedy już coś udowodnimy, jesteśmy absolutnie pewni, że to jest i zawsze będzie prawdziwe. Nie jest to tylko teoria, która pasuje do naszych obserwacji i może być zastąpiona przez lepszą teorię w przyszłości.
W powyższym przykładzie moglibyśmy policzyć liczbę przecięć we wnętrzu koła. Dokładne zastanowienie się nad związkiem między liczbą przecięć, linii i regionów doprowadzi nas w końcu do innego równania na liczbę regionów, gdy istnieje x = V.Axi punktów na okręgu:
Liczba regionów = x4 – 6 x3 + 23 x2 – 18 x + 2424 = (Math.pow(V.Axi,4) – 6*Math.pow(V.Axi,3) + 23*Math.pow(V.Axi,2) – 18*V.Axi + 24)/24.
Równanie to działa we wszystkich powyższych przypadkach. Możemy teraz spróbować udowodnić je dla każdej wartości x używając „indukcji”, techniki wyjaśnionej poniżej.
Tradycyjnie, koniec dowodu wskazuje się używając ■ lub □, lub pisząc QED lub „quod erat demonstrandum”, co po łacinie oznacza „co należało pokazać”.
Wynik lub obserwacja, która naszym zdaniem jest prawdziwa nazywana jest Hipotezą lub Przypuszczeniem. Kiedy już to udowodnimy, nazywamy to Twierdzeniem. Gdy udowodnimy twierdzenie, możemy użyć go do udowodnienia innych, bardziej skomplikowanych wyników – budując w ten sposób rosnącą sieć twierdzeń matematycznych.
Aksjomaty

Szkoła Ateńska Rafaela: starożytni greccy matematycy byli pierwszymi, którzy podeszli do matematyki używając logicznych i aksjomatycznych ram.
Jednym z interesujących pytań jest to, od czego zacząć. Jak udowodnić pierwsze twierdzenie, jeśli jeszcze nic nie wiemy? Niestety nie można udowodnić czegoś używając niczego. Potrzebujesz co najmniej kilku elementów konstrukcyjnych, od których możesz zacząć, a te nazywane są aksjomatami.
Matematycy zakładają, że aksjomaty są prawdziwe bez możliwości ich udowodnienia. Jednak to nie jest tak problematyczne, jak może się wydawać, ponieważ aksjomaty są albo definicje lub wyraźnie oczywiste, i istnieje tylko bardzo niewiele aksjomatów. Na przykład, aksjomat może być, że a + b = b + a dla dowolnych dwóch liczb a i b.
Aksjomaty są ważne, aby uzyskać prawo, ponieważ cała matematyka opiera się na nich. Jeśli jest zbyt mało aksjomatów, można udowodnić bardzo niewiele i matematyka nie byłaby zbyt interesująca. Jeśli jest zbyt wiele aksjomatów, można udowodnić prawie wszystko i matematyka również nie byłaby interesująca. Nie można też mieć aksjomatów sprzecznych ze sobą.
Matematyka nie polega na wyborze właściwego zestawu aksjomatów, ale na rozwijaniu ram z tych punktów wyjścia. Jeśli zaczniesz z różnymi aksjomatami, otrzymasz inny rodzaj matematyki, ale logiczne argumenty będą takie same. Każda dziedzina matematyki ma swój własny zestaw podstawowych aksjomatów.
Gdy matematycy udowodnią jakieś twierdzenie, publikują je dla innych matematyków do sprawdzenia. Czasami znajdują błąd w logicznym argumencie, a czasami błąd nie jest znaleziony aż do wielu lat później. Jednakże, w zasadzie, zawsze jest możliwe rozbicie dowodu na podstawowe aksjomaty.
Teoria zbiorów i aksjomat wyboru

Aby sformułować dowód, trzeba czasem wrócić do samego fundamentu języka, w którym zapisana jest matematyka: teorii zbiorów.
Zbiór to zbiór obiektów, takich jak liczby. Elementy zbioru są zwykle zapisywane w nawiasach klamrowych. Możemy znaleźć unię dwóch zbiorów (zbiór elementów, które są w każdym ze zbiorów) lub możemy znaleźć przecięcie dwóch zbiorów (zbiór elementów, które są w obu zbiorach).
Wiele problemów matematycznych można sformułować w języku teorii zbiorów, a do ich udowodnienia potrzebne są aksjomaty teorii zbiorów. Z biegiem czasu matematycy używali różnych zbiorów aksjomatów, z których najszerzej akceptowane jest dziewięć aksjomatów Zermelo-Fraenkela (ZF):
AKSJOMAT ROZSZERZENIA
Jeśli dwa zbiory mają te same elementy, to są równe.
AXIOM OF SEPARATION
Możemy utworzyć podzbiór zbioru, który składa się z pewnych elementów.

AKSYMAT ZBIORU
Istnieje zbiór bez elementów, zapisywany jako {} lub ∅.
PAIR-SET AXIOM
Dając dwa obiekty x i y możemy utworzyć zbiór {x, y}.
UNION AXIOM
Możemy utworzyć unię dwóch lub więcej zbiorów.
OSIOM ZBIORÓW POTĘGOWYCH
Dając dowolny zbiór, możemy utworzyć zbiór wszystkich podzbiorów (zbiór potęgowy).
OSIOM NIEFINITY
Istnieje zbiór o nieskończenie wielu elementach.

AKSYMAT FUNDACJI
Zbiory są zbudowane z prostszych zbiorów, co oznacza, że każdy (niepusty) zbiór ma minimalnego członka.
AKSYMAT ZASTĄPIENIA
Jeśli zastosujemy funkcję do każdego elementu w zbiorze, odpowiedź nadal jest zbiorem.
Jeśli myślisz o teorii zbiorów, większość z tych aksjomatów wyda ci się zupełnie oczywista – i takie właśnie powinny być aksjomaty. Istnieje jednak dziesiąty aksjomat, który jest raczej bardziej problematyczny:
AKSJOM WYBORU
Dając nieskończenie wiele niepustych zbiorów, można wybrać jeden element z każdego z tych zbiorów.
Na pierwszy rzut oka aksjomat wyboru (AC) wygląda tak samo niewinnie jak inne powyższe. Jednak użycie nieskończoności ma wiele nieoczekiwanych konsekwencji. Na przykład, można użyć AC do udowodnienia, że możliwe jest pocięcie kuli na pięć kawałków i ponowne złożenie ich tak, aby powstały dwie kule, z których każda jest identyczna z kulą początkową. Jest to tylko teoretyczna koncepcja – wymagane cięcia są fraktalne, co oznacza, że nie mogą istnieć w prawdziwym życiu, a niektóre z kawałków są „niemierzalne”, co oznacza, że nie mają zdefiniowanej objętości. Ale fakt, że aksjomat wyboru może być użyty do skonstruowania tych niemożliwych cięć jest dość niepokojący.
Wśród logików toczy się namiętna debata, czy zaakceptować aksjomat wyboru, czy nie. Każdy zbiór aksjomatów tworzy mały „świat matematyczny”, a różne twierdzenia mogą być prawdziwe w różnych światach. Jest to naprawdę tylko kwestia tego, czy jesteś szczęśliwy żyjąc w świecie, w którym możesz zrobić dwie kule z jednej…
Dowód przez indukcję
Dowód przez indukcję jest techniką, która może być użyta do udowodnienia, że pewne stwierdzenie jest prawdziwe dla wszystkich liczb naturalnych 1, 2, 3, … „Stwierdzenie” jest zwykle równaniem lub formułą, która zawiera zmienną n, która może być dowolną liczbą naturalną. Oznaczmy twierdzenie zastosowane do n przez S(n). Oto cztery kroki indukcji matematycznej:
- Najpierw dowodzimy, że S(1) jest prawdziwe, tzn. że twierdzenie S jest prawdziwe dla 1.
- Teraz zakładamy, że S(k) jest prawdziwe, tzn. że twierdzenie S jest prawdziwe dla pewnej liczby naturalnej k.
- Korzystając z tego założenia, próbujemy wydedukować, że S(k + 1) jest również prawdziwe. Zatem zawsze, gdy S jest prawdziwe dla jednej liczby, jest również prawdziwe dla następnej liczby.
- Ponieważ wiemy, że S(1) jest prawdziwe, S(2) musi być prawdziwe. I dlatego S(3) musi być prawdziwe. I dlatego S(4) musi być prawdziwe. I tak dalej: S musi być prawdziwe dla wszystkich liczb.

Indukcję można porównać do spadającego domina: ilekroć jedno domino upada, następne również upada. Pierwszy krok, udowodnienie, że S(1) jest prawdziwe, rozpoczyna nieskończoną reakcję łańcuchową.
Pierwszy krok jest często pomijany, ponieważ jest tak prosty. W rzeczywistości jest on bardzo ważny i zależy od niego cały łańcuch indukcyjny – jak pokażą niektóre z poniższych przykładów…
Celem gry Wieże Hanoi jest przeniesienie pewnej liczby dysków z jednego kołka na drugi. Możesz przenieść tylko jeden dysk na raz i nie możesz umieścić większego dysku na mniejszym. Spróbuj przenieść wieżę z dysków z pierwszego kołka na ostatni kołek, wykonując jak najmniej ruchów:
Liczba dysków: Start Over Moves: 0
Gdy już zrozumiemy zasady gry, możemy spróbować znaleźć najmniejszą liczbę niezbędnych kroków, biorąc pod uwagę dowolną liczbę dysków. Zabawa z powyższą grą może nas doprowadzić do spostrzeżenia, że mając n krążków, potrzebujemy co najmniej 2n – 1 kroków. Nazwijmy to stwierdzenie S(n).
S(1) jest oczywiście prawdziwe, ponieważ mając tylko jeden dysk, potrzebujemy tylko jednego ruchu, a 21 – 1 = 1.
Załóżmy teraz, że S(k) jest prawdziwe, tzn. że dla k dysków potrzebujemy 2k – 1 kroków. Wówczas, jeśli mamy k + 1 dysków:
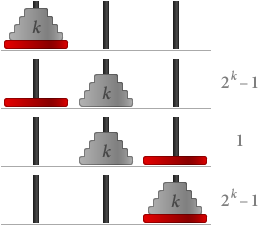
W sumie potrzebujemy (2k – 1) + 1 + (2k – 1) = 2(k+1) – 1 kroków. Oznacza to, że S(k + 1) jest również prawdziwe.
Przez indukcję matematyczną, S(n) jest prawdziwe dla wszystkich wartości n, co oznacza, że najbardziej efektywny sposób przesunięcia n = V.Hanoi dysków wymaga 2n – 1 = Math.pow(2,V.Hanoi)-1 ruchów. ■
Wykorzystajmy indukcję do udowodnienia, że suma pierwszych n liczb naturalnych wynosi n (n + 1)2. Najpierw sprawdzamy równanie dla małych wartości n:
1 = 1 (1 + 1)2.
1 + 2 = 2 (2 + 1)2 = 3.
Następnie zakładamy, że wynik jest prawdziwy dla k, tzn. że 1 + 2 + … + k = k (k + 1)2, gdzie k jest jakąś liczbą, której nie podajemy. Teraz
1 + 2 + … + k + (k + 1) = k (k + 1)2 + (k + 1) = (k + 1) (k + 2)2 = (k + 1) 2.
Dowiedliśmy właśnie, że jeśli równanie jest prawdziwe dla jakiegoś k, to jest też prawdziwe dla k + 1. Przez indukcję matematyczną równanie jest prawdziwe dla wszystkich wartości n. ■
Jest jeszcze jeden sprytny sposób udowodnienia powyższego równania, który nie wykorzystuje indukcji. Podobno Carl Friedrich Gauss (1777 – 1855), jeden z największych matematyków w historii, odkrył tę metodę w szkole podstawowej, gdy jego nauczyciel poprosił go o zsumowanie wszystkich liczb całkowitych od 1 do 100.
Używając indukcji, chcemy udowodnić, że wszyscy ludzie mają taki sam kolor włosów. Niech S(n) będzie stwierdzeniem, że „dowolna grupa n istot ludzkich ma ten sam kolor włosów”.
Jasno widać, że S(1) jest prawdziwe: w dowolnej grupie złożonej tylko z jednego człowieka wszyscy mają ten sam kolor włosów.
Załóżmy teraz S(k), że w dowolnej grupie złożonej z k osób wszyscy mają ten sam kolor włosów. Jeśli zastąpimy kogokolwiek w grupie kimś innym, to nadal tworzą oni w sumie k, a więc mają ten sam kolor włosów. Działa to dla dowolnej początkowej grupy osób, co oznacza, że każda grupa k + 1 również ma ten sam kolor włosów. Zatem S(k + 1) jest prawdziwe.
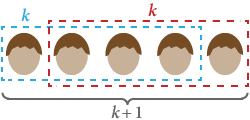
Przez indukcję matematyczną, wszyscy ludzie mają ten sam kolor włosów!
Najwyraźniej coś musiało pójść nie tak w powyższym dowodzie – przecież nie wszyscy mają taki sam kolor włosów. Czy potrafisz znaleźć ten błąd?
Niektórych twierdzeń nie da się udowodnić za pomocą indukcji – musimy użyć nieco zmodyfikowanej wersji zwanej Silną Indukcją. Zamiast zakładać S(k), by udowodnić S(k + 1), zakładamy wszystkie S(1), S(2), … S(k), by udowodnić S(k + 1). Wszystko, co może być udowodnione przy użyciu (słabej) indukcji, może być również udowodnione przy użyciu silnej indukcji, ale nie odwrotnie.
Podstawowe twierdzenie arytmetyki stwierdza, że każda liczba całkowita większa od 1 jest albo liczbą pierwszą, albo może być zapisana jako iloczyn liczb pierwszych w sposób zasadniczo unikalny.
Możemy udowodnić jego część używając silnej indukcji: niech S(n) będzie stwierdzeniem, że „liczba całkowita n jest liczbą pierwszą lub może być zapisana jako iloczyn liczb pierwszych”. S(1) jest wyjątkiem, ale S(2) jest oczywiście prawdziwe, bo 2 jest liczbą pierwszą.
Załóżmy teraz, że S(1), S(2), …, S(k) są wszystkie prawdziwe, dla jakiejś liczby całkowitej k. Wiemy, że k + 1 jest albo liczbą pierwszą, albo ma czynniki mniejsze niż k + 1. Z naszego założenia wiemy, że te czynniki mogą być zapisane jako iloczyn liczb pierwszych. Zatem k + 1, o ile nie jest liczbą pierwszą, może być również zapisane jako iloczyn liczb pierwszych. Oznacza to, że S(k + 1) jest prawdziwe.
Przez silną indukcję, S(n) jest prawdziwe dla wszystkich liczb n większych od 1. ■
Udowodnienie, że ta faktoryzacja liczb pierwszych jest unikalna (chyba, że liczymy różne uporządkowania czynników) wymaga więcej pracy, ale nie jest szczególnie trudne.
Okazuje się, że zasada słabej indukcji i zasada silnej indukcji są równoważne: każda implikuje drugą. Obie są też równoważne trzeciemu twierdzeniu, zasadzie dobrego uporządkowania: każdy (niepusty) zbiór liczb naturalnych ma element minimalny, mniejszy od wszystkich pozostałych.
Zasada dobrego uporządkowania jest cechą definiującą liczby naturalne. Jest to jeden z podstawowych aksjomatów używanych do definiowania liczb naturalnych ![]() = {1, 2, 3, …}. Aksjomaty te nazywane są aksjomatami Peano, od nazwiska włoskiego matematyka Guiseppe Peano (1858 – 1932).
= {1, 2, 3, …}. Aksjomaty te nazywane są aksjomatami Peano, od nazwiska włoskiego matematyka Guiseppe Peano (1858 – 1932).
Dowód przez sprzeczność
Dowód przez sprzeczność jest kolejną ważną techniką dowodową. Jeśli chcemy udowodnić twierdzenie S, to zakładamy, że S nie było prawdziwe. Wykorzystując to założenie próbujemy wydedukować fałszywy wynik, np. 0 = 1. Jeśli wszystkie nasze kroki były poprawne, a wynik jest fałszywy, to nasze początkowe założenie musiało być błędne. Naszym początkowym założeniem było, że S nie jest prawdziwe, co oznacza, że S faktycznie jest prawdziwe.
Tej techniki można użyć w wielu różnych okolicznościach, takich jak udowodnienie, że √2 jest irracjonalne, udowodnienie, że liczby rzeczywiste są niepoliczalne, lub udowodnienie, że istnieje nieskończenie wiele liczb pierwszych.
Oto kolejny zabawny przykład:
Możemy użyć dowodu przez sprzeczność, wraz z zasadą porządkującą, aby udowodnić, że wszystkie liczby naturalne są „interesujące”.
Załóżmy, że nie wszystkie liczby naturalne są interesujące i niech S będzie zbiorem liczb nieinteresujących. Przez zasadę porządkującą, S ma najmniejszego członka x, który jest najmniejszą liczbą nieinteresującą. Ta ciekawa własność wyraźnie czyni x szczególnie interesującą liczbą. Jest to sprzeczność, ponieważ założyliśmy, że x jest nieinteresująca.
Więc wszystkie liczby są interesujące. ■
Gödel and Unprovable Theorems

Kurt Gödel (1906-1978)
Na początku XX wieku matematyka zaczęła się gwałtownie rozwijać, tysiące matematyków pracowało w niezliczonych nowych dziedzinach. David Hilbert (1862 – 1943) stworzył obszerny program formalizacji matematyki i rozwiązania wszelkich niespójności w podstawach matematyki. Obejmował on udowodnienie wszystkich twierdzeń przy użyciu zestawu prostych i uniwersalnych aksjomatów, udowodnienie, że ten zestaw aksjomatów jest spójny, oraz udowodnienie, że ten zestaw aksjomatów jest kompletny, tzn. że każde twierdzenie matematyczne może być udowodnione lub obalone przy użyciu aksjomatów.
Niestety, plany te zostały zniszczone przez Kurta Gödla w 1931 roku. Udowodnił on, że w każdym (dostatecznie złożonym) systemie matematycznym z pewnym zestawem aksjomatów można znaleźć pewne twierdzenia, których nie da się ani udowodnić, ani obalić za pomocą tych aksjomatów. Nie można też udowodnić, że pewien zbiór aksjomatów jest spójny, nie używając niczego poza samymi aksjomatami.
Odkrycie Gödla opiera się na fakcie, że zbiór aksjomatów nie może być użyty do powiedzenia czegokolwiek o sobie, np. czy jest spójny. Problemy z autoreferencją można znaleźć nie tylko w matematyce, ale także w języku. Oto Paradoks Kłamcy:
„To zdanie jest fałszywe.”
Zdanie powyżej próbuje powiedzieć coś o sobie. Jeśli jest prawdziwe, to zdanie mówi nam, że jest fałszywe. Jeśli jest fałszywe, to zdanie mówi nam, że nie jest fałszywe, tzn. że jest prawdziwe. W efekcie zdanie nie jest ani prawdziwe, ani fałszywe.
Gdy po raz pierwszy opublikowane, twierdzenia Gödla były głęboko niepokojące dla wielu matematyków. Przystępując do udowadniania obserwacji, nie wiemy, czy dowód istnieje – wynik może być prawdziwy, ale nieudowodniony. Dziś wiemy, że niezupełność jest fundamentalną częścią nie tylko logiki, ale także informatyki, która opiera się na maszynach wykonujących operacje logiczne.
Zaskakująco, możliwe jest udowodnienie, że pewne stwierdzenia są nie do udowodnienia. Jednym z przykładów jest Hipoteza Continuum, która dotyczy wielkości nieskończonych zbiorów.
Pod koniec życia Kurt Gödel rozwinął poważne problemy psychiczne i zmarł z głodu w 1978 roku. Jego spostrzeżenia dotyczące podstaw logiki były najgłębsze od czasu rozwoju dowodu przez starożytnych Greków.
.