
Bertrand Russell (1872-1970) i A.N. Whitehead (1861-1947)
Bertrand Russell i Alfred North Whitehead byli brytyjskimi matematykami, logikami i filozofami, którzy byli w awangardzie brytyjskiej rewolty przeciwko kontynentalnemu idealizmowi na początku XX wieku i, między nimi, wnieśli ważny wkład w dziedzinie logiki matematycznej i teorii zbiorów.
Whitehead był starszy z nich dwóch i pochodził z bardziej czystej matematyki background. Został nauczycielem Russella w Trinity College w Cambridge w latach 90. XIX wieku, a następnie współpracował z jego sławniejszym byłym uczniem w pierwszej dekadzie XX wieku nad ich monumentalnym dziełem, „Principia Mathematica”. Jednak po I wojnie światowej, którą Russell spędził w więzieniu ze względu na swoją działalność pacyfistyczną, współpraca wygasła, a kariera akademicka Whiteheada pozostała na zawsze w cieniu kariery bardziej krzykliwego Russella. W latach 20. wyemigrował do Stanów Zjednoczonych i tam spędził resztę życia.
Russell urodził się w zamożnej rodzinie brytyjskiej arystokracji, choć jego rodzice byli niezwykle liberalni i radykalni jak na tamte czasy. Jego rodzice zmarli, gdy Russell był dość młody, a on był w dużej mierze wychowywany przez jego zagorzałych wiktoriańskich (choć dość postępowe) babci. W okresie dojrzewania był bardzo samotny i cierpiał na ataki depresji, twierdząc później, że tylko miłość do matematyki uchroniła go przed samobójstwem. Studiował matematykę i filozofię na Uniwersytecie Cambridge pod kierunkiem G.E. Moore’a i A.N. Whiteheada, gdzie rozwinął się w nowatorskiego filozofa, płodnego pisarza na wiele tematów, zdeklarowanego ateistę oraz natchnionego matematyka i logika. Dziś jest uważany za jednego z założycieli filozofii analitycznej, ale pisał na prawie każdym głównym obszarze filozofii, zwłaszcza metafizyki, etyki, epistemologii, filozofii matematyki i filozofii języka.
Russell był zaangażowany i wysokiej rangi działacz polityczny przez całe swoje długie życie. Był wybitnym działaczem antywojennym zarówno podczas pierwszej, jak i drugiej wojny światowej, orędownikiem wolnego handlu i antyimperializmu, a później stał się zdecydowanym bojownikiem o rozbrojenie nuklearne i socjalizm, a także przeciwko Adolfowi Hitlerowi, sowieckiemu totalitaryzmowi i zaangażowaniu USA w wojnę wietnamską.
Russell’s Paradox
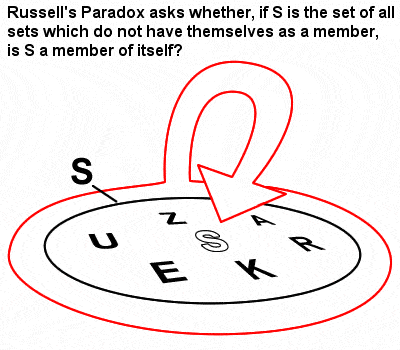
Russell’s Paradox
Matematyka Russella była pod wielkim wpływem teorii zbiorów i logiki, które Gottlob Frege rozwinął w następstwie przełomowej wczesnej pracy Cantora o zbiorach. W swoich „The Principles of Mathematics” z 1903 roku zidentyfikował jednak to, co stało się znane jako Paradoks Russella (zbiór zawierający zbiory, które nie są członkami samych siebie), który pokazał, że naiwna teoria zbiorów Fregego może w rzeczywistości prowadzić do sprzeczności.
Paradoks jest czasami ilustrowany przez ten uproszczony przykład: „Jeśli fryzjer goli wszystkich i tylko tych mężczyzn we wsi, którzy nie golą się sami, to czy goli samego siebie?”
Paradoks zdawał się sugerować, że nie można już ufać samym podstawom całej matematyki i że nawet w matematyce nigdy nie można absolutnie poznać prawdy (późniejsze prace Gödla i Turinga tylko pogorszyłyby ten stan rzeczy). Krytyka Russella wystarczyła, by zachwiać zaufaniem Fregego do całego gmachu logicyzmu, a on sam był na tyle łaskawy, by przyznać to otwarcie w pospiesznie napisanym dodatku do II tomu swoich „Podstawowych praw arytmetyki”.
Ale magnum opus Russella było monolityczne „Principia Mathematica”, opublikowane w trzech tomach w latach 1910, 1912 i 1913. Pierwszy tom był współtworzony przez Whiteheada, choć dwa późniejsze były niemal w całości dziełem Russella. Celem tego ambitnego dzieła była próba wyprowadzenia całej matematyki z czysto logicznych aksjomatów, przy jednoczesnym uniknięciu paradoksów i sprzeczności, jakie można było znaleźć we wcześniejszych pracach Fregego na temat teorii zbiorów. Russell osiągnął to dzięki zastosowaniu teorii lub systemu „typów”, w którym każdemu bytowi matematycznemu przypisany jest typ w ramach hierarchii typów, tak że obiekty danego typu budowane są wyłącznie z obiektów poprzedzających je typów znajdujących się niżej w hierarchii, co zapobiega powstawaniu pętli. Każdy zbiór elementów jest więc innego typu niż każdy z jego elementów, tak że nie można mówić o „zbiorze wszystkich zbiorów” i podobnych konstrukcjach, które prowadzą do paradoksów.
Jednakże „Principia” wymagały, oprócz podstawowych aksjomatów teorii typów, trzech dalszych aksjomatów, które wydawały się nie być prawdziwe jako zwykłe sprawy logiki, a mianowicie „aksjomatu nieskończoności” (który gwarantuje istnienie co najmniej jednego nieskończonego zbioru, mianowicie zbioru wszystkich liczb naturalnych), „aksjomatu wyboru” (który zapewnia, że biorąc pod uwagę dowolny zbiór „pojemników”, z których każdy zawiera co najmniej jeden obiekt, możliwe jest dokonanie wyboru dokładnie jednego obiektu z każdego kosza, nawet jeśli jest ich nieskończenie wiele, i że nie istnieje żadna „reguła” dotycząca tego, który obiekt wybrać z każdego z nich) oraz Russella własny „aksjomat redukowalności” (który stwierdza, że dowolna propozycjonalna funkcja prawdy może być wyrażona przez formalnie równoważną predykatywną funkcję prawdy).
Podczas około dziesięciu lat, które Russell i Whitehead spędzili nad „Principiami”, szkic za szkicem był rozpoczynany i porzucany, ponieważ Russell ciągle na nowo rozważał swoje podstawowe założenia. Russell i jego żona Alys zamieszkali nawet z Whiteheadami, aby przyspieszyć prace, choć jego własne małżeństwo ucierpiało, gdy Russell zadurzył się w młodej żonie Whiteheada, Evelyn. Ostatecznie Whitehead nalegał na publikację dzieła, nawet jeśli nie było ono (i może nigdy nie będzie) kompletne, choć byli zmuszeni wydać je na własny koszt, gdyż żadne komercyjne wydawnictwo nie chciało go tknąć.
Principia Mathematica

Mała część długiego dowodu, że 1+1 =2 w „Principia Mathematica”
Jakieś pojęcie o zakresie i wszechstronności „Principia” można uzyskać z faktu, że ostateczne udowodnienie, że 1 + 1 = 2 zajmuje ponad 360 stron.
Dzisiaj jest ono powszechnie uważane za jedno z najważniejszych i najbardziej przełomowych dzieł logiki od czasu „Organonu” Arystotelesa. Wydawało się ono niezwykle udane i odporne w swych ambitnych celach, a wkrótce zyskało światową sławę dzięki Russellowi i Whiteheadowi. W rzeczy samej, dopiero twierdzenie niezupełności Gödla z 1931 roku ostatecznie pokazało, że „Principia” nie mogą być zarówno spójne, jak i kompletne.
Russell został odznaczony Orderem Zasługi w 1949 roku, a w następnym roku otrzymał Nagrodę Nobla w dziedzinie literatury. Jego sława nadal rosła, nawet poza kręgami akademickimi, a on stał się czymś w rodzaju nazwiska domowego w późniejszym życiu, choć głównie w wyniku jego wkładów filozoficznych i jego aktywizm polityczny i społeczny, który kontynuował do końca swojego długiego życia. Zmarł na grypę w swojej ukochanej Walii w sędziwym wieku 97 lat.
| << Powrót do Hardy’ego i Ramanujana | Przód do Hilberta >> |
.