Matice je pole čísel:

Matice
(Tato má 2 řádky a 3 sloupce)
Násobit matici jedním číslem je snadné:
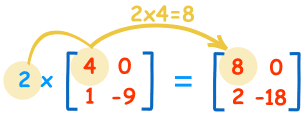
| 2×4=8 | 2×0=0 |
| 2×1=2 | 2×-9=-18 |
Číslu („2“ v tomto případě) říkáme skalár, proto se tomu říká „skalární násobení“.
Násobení matice jinou maticí
Ale abychom vynásobili matici jinou maticí, musíme provést „bodový součin“ řádků a sloupců … co to znamená? Podívejme se na to na příkladu:
Připravíme si odpověď pro 1. řádek a 1. sloupec:
„Bodový součin“ je to, když vynásobíme odpovídající členy a pak sečteme:
(1, 2, 3) – (7, 9, 11) = 1×7 + 2×9 + 3×11
= 58
Shodujeme 1. členy (1 a 7), vynásobíme je, stejně tak 2. členy (2 a 9) a 3. členy (3 a 11) a nakonec je sečteme.
Chcete vidět další příklad? Zde je pro 1. řádek a 2. sloupec:
(1, 2, 3) – (8, 10, 12) = 1×8 + 2×10 + 3×12
= 64
To samé můžeme udělat pro 2. řádek a 1. sloupec:
(4, 5, 6) – (7, 9, 11) = 4×7 + 5×9 + 6×11
= 139
A pro 2. řádek a 2. sloupec:
(4, 5, 6) – (8, 10, 12) = 4×8 + 5×10 + 6×12
= 154
A dostáváme:
PROČ!
Proč to dělat tímto způsobem?“
Může se to zdát jako zvláštní a složitý způsob násobení, ale je to nutné!“
Můžu uvést příklad ze života, který ilustruje, proč násobíme matice tímto způsobem.
Příklad: Místní obchod prodává 3 druhy koláčů.
- Jablečný koláč stojí 3 dolary za kus
- Třešňový koláč stojí 4 dolary za kus
- Boruvkový koláč stojí 2 dolary za kus
A toto je počet, který prodali za 4 dny:
Nyní se zamyslete nad tímto … hodnota prodeje za pondělí se vypočítá takto:
Takže je to vlastně „bodový součin“ cen a toho, kolik se prodalo:
($3, $4, $2) – (13, 8, 6) = $3×13 + $4×8 + $2×6
= $83
Přizpůsobíme cenu tomu, kolik se prodalo, vynásobíme každou z nich a výsledek sečteme.
Jinými slovy:
- Prodej za pondělí byl: Jablečné koláče: 3×13=39 dolarů, třešňové koláče: 4×8=32 dolarů a borůvkové koláče: 2×6=12 dolarů. Dohromady to je 39 $ + 32 $ + 12 $ = 83 $
- A za úterý: 3×9 $ + 4×7 $ + 2×4 $ = 63 $
- A za středu: 3×7 $ + 4×4 $ + 2×0 $ = 37 $
- A za čtvrtek: 3×15 $ + 4×6 $ + 2×3 $ = 75 $
Je tedy důležité, aby každá cena odpovídala každému množství.
Teď už víte, proč používáme „bodový součin“.
A zde je celý výsledek v maticovém tvaru:

V pondělí prodali koláče za 83 dolarů, v úterý za 63 dolarů atd.
(Tyto hodnoty můžete vložit do maticové kalkulačky a zjistit, zda fungují.)
Řádky a sloupce
Pro znázornění, kolik má matice řádků a sloupců, často píšeme řádky×sloupce.
Příklad: Tato matice je 2×3 (2 řádky po 3 sloupcích):
Při násobení:
- Počet sloupců 1. matice se musí rovnat počtu řádků 2. matice.
- A výsledek bude mít stejný počet řádků jako 1. matice a stejný počet sloupců jako 2. matice.
Příklad:

V tomto příkladu jsme násobili matici 1×3 maticí 3×4 (všimněte si, že trojky jsou stejné) a výsledkem byla matice 1×4.
Obecně:
Chceme-li vynásobit matici m×n maticí n×p, musí být ns stejné,
a výsledkem je matice m×p.
![]()
Takže … vynásobením matice 1×3 maticí 3×1 získáme výsledek 1×1:
Ale vynásobením 3×1 číslem 1×3 dostaneme výsledek 3×3:
Identitní matice
„Identitní matice“ je maticový ekvivalent čísla „1“:
Matice identity 3×3
- Je „čtvercová“ (má stejný počet řádků jako sloupců)
- Může být velká nebo malá (2×2, 100×100, … cokoli)
- Na hlavní diagonále má 1 a všude jinde 0
- Její symbol je velké písmeno I
Je to zvláštní matice, protože když jí vynásobíme, původní se nezmění:
A × I = A
I × A = A
Pořadí násobení
V aritmetice jsme zvyklí:
3 × 5 = 5 × 3
(komutativní zákon násobení)
Pro matice to však obecně neplatí (násobení matic není komutativní):
AB ≠ BA
Když změníme pořadí násobení, odpověď je (obvykle) jiná.
Příklad:
Podívejte se, jak změna pořadí ovlivní toto násobení:
Odpovědi jsou různé!
Může to mít stejný výsledek (například když je jedna matice maticí identity), ale obvykle ne.




