En matris är en matris av siffror:

En matris
(Den här matrisen har 2 rader och 3 kolumner)
Det är enkelt att multiplicera en matris med ett enskilt tal:
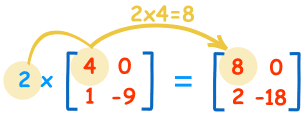
| 2×4=8 | 2×0=0 |
| 2×1=2 | 2×-9=-18 |
Vi kallar talet (”2” i det här fallet) för en skalär, så det kallas för ”skalär multiplikation”.
Multiplicering av en matris med en annan matris
Men för att multiplicera en matris med en annan matris måste vi göra ”punktprodukten” av rader och kolumner … vad betyder det? Låt oss se med ett exempel:
För att räkna ut svaret för 1:a raden och 1:a kolumnen:
Den s.k. ”prickprodukten” innebär att vi multiplicerar matchande delar och sedan summerar:
(1, 2, 3) – (7, 9, 11) = 1×7 + 2×9 + 3×11
= 58
Vi matchar de första delarna (1 och 7), multiplicerar dem, likaså de andra delarna (2 och 9) och de tredje delarna (3 och 11), och summerar dem slutligen.
Vill du se ett annat exempel? Här är det för 1:a raden och 2:a kolumnen:
(1, 2, 3) – (8, 10, 12) = 1×8 + 2×10 + 3×12
= 64
Vi kan göra samma sak för 2:a raden och 1:a kolumnen:
(4, 5, 6) – (7, 9, 11) = 4×7 + 5×9 + 6×11
= 139
Och för andra raden och andra kolumnen:
(4, 5, 6) – (8, 10, 12) = 4×8 + 5×10 + 6×12
= 154
Och vi får:
DONE!
Varför gör vi så här?
Detta kan tyckas vara ett konstigt och komplicerat sätt att multiplicera, men det är nödvändigt!
Jag kan ge dig ett exempel från verkligheten för att illustrera varför vi multiplicerar matriser på det här sättet.
Exempel:
- Äppelpajer kostar 3 dollar styck
- Körsbärspajer kostar 4 dollar styck
- Blåbärspajer kostar 2 dollar styck
Och så här många sålde de på 4 dagar:
Tänk på det här … värdet av försäljningen för måndagen beräknas på följande sätt:
Det är alltså i själva verket ”punktprodukten” av priserna och hur många som såldes:
($3, $4, $2) – (13, 8, 6) = $3×13 + $4×8 + $2×6
= $83
Vi matchar priset med hur många som sålts, multiplicerar varje pris och summerar sedan resultatet.
Med andra ord:
- Försäljningen för måndagen var: Äppelpajer: 3×13=39 dollar, körsbärspajer: 4×8=32 dollar och blåbärspajer: 2×6=12 dollar. Tillsammans blir det 39$ + 32$ + 12$ = 83$
- Och för tisdag: $3×9 + $4×7 + $2×4 = 63$
- Och för onsdag: $3×7 + $4×4 + $2×0 = 37$
- Och för torsdag: $3×15 + $4×6 + $2×3 = 75$
Det är alltså viktigt att matcha varje pris med varje mängd.
Nu vet du varför vi använder ”punktprodukten”.
Och här är det fullständiga resultatet i matrisform:

De sålde pajer för 83 dollar i måndags, 63 dollar i tisdags osv.
(Du kan lägga in dessa värden i matrisräknaren för att se om de fungerar.)
Rader och kolumner
För att visa hur många rader och kolumner en matris har skriver vi ofta rader×kolumner.
Exempel: När vi multiplicerar:
- Antalet kolumner i den första matrisen måste vara lika med antalet rader i den andra matrisen.
- Och resultatet kommer att ha samma antal rader som den första matrisen och samma antal kolumner som den andra matrisen.
Exempel:

I det exemplet multiplicerade vi en 1×3-matris med en 3×4-matris (observera att 3:orna är desamma), och resultatet blev en 1×4-matris.
I allmänhet:
För att multiplicera en m×n-matris med en n×p-matris måste ns vara desamma,
och resultatet är en m×p-matris.
![]()
Så … att multiplicera en 1×3 med en 3×1 ger ett 1×1-resultat:
Men om man multiplicerar ett 3×1 med ett 1×3 så får man ett 3×3 resultat:
Identitetsmatris
”Identitetsmatrisen” är matrisens motsvarighet till talet ”1”:
En 3×3 identitetsmatris
- Den är ”kvadratisk” (har samma antal rader som kolumner)
- Den kan vara stor eller liten (2×2, 100×100, … whatever)
- Den har 1:or på huvuddiagonalen och 0:or överallt annars
- Dess symbol är den stora bokstaven I
Det är en speciell matris, för när vi multiplicerar med den är originalet oförändrat:
A × I = A
I × A = A
Multiplikationsordning
I aritmetiken är vi vana vid:
3 × 5 = 5 × 3
(Den kommutativa lagen om multiplikation)
Men detta gäller i allmänhet inte för matriser (matrismultiplikation är inte kommutativ):
AB ≠ BA
När vi ändrar multiplikationens ordning blir svaret (vanligtvis) annorlunda.
Exempel:
Se hur en ändring av ordningen påverkar denna multiplikation:
Svaren är olika!
Det kan ge samma resultat (t.ex. när en matris är identitetsmatrisen) men vanligtvis inte.




