En matrix er en række tal:

En matrix
(Denne matrix har 2 rækker og 3 kolonner)
Det er nemt at multiplicere en matrix med et enkelt tal:
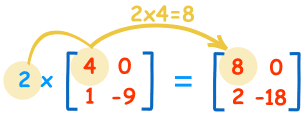
| 2×4=8 | 2×0=0 |
| 2×1=2 | 2×-9=-18 |
Vi kalder tallet (“2” i dette tilfælde) for en skalar, så dette kaldes “skalar multiplikation”.
Multiplikation af en matrix med en anden matrix
Men for at multiplicere en matrix med en anden matrix skal vi lave “prikproduktet” af rækker og kolonner … hvad betyder det? Lad os se det med et eksempel:
For at udregne svaret for 1. række og 1. kolonne:
Det “prikprodukt” er, hvor vi multiplicerer matchende medlemmer og derefter summerer op:
(1, 2, 3) – (7, 9, 11) = 1×7 + 2×9 + 3×11
= 58
Vi matcher 1. led (1 og 7), ganger dem, ganger dem på samme måde med 2. led (2 og 9) og 3. led (3 og 11), og til sidst summerer vi dem op.
Vil du se et andet eksempel? Her er det for 1. række og 2. kolonne:
(1, 2, 3) – (8, 10, 12) = 1×8 + 2×10 + 3×12
= 64
Vi kan gøre det samme for 2. række og 1. kolonne:
(4, 5, 6) – (7, 9, 11) = 4×7 + 5×9 + 6×11
= 139
Og for den 2. række og 2. kolonne:
(4, 5, 6) – (8, 10, 12) = 4×8 + 5×10 + 6×12
= 154
Og vi får:
DONE!
Hvorfor gør vi det på denne måde?
Dette kan virke som en mærkelig og kompliceret måde at gange på, men det er nødvendigt!
Jeg kan give dig et eksempel fra det virkelige liv for at illustrere, hvorfor vi multiplicerer matricer på denne måde.
Eksempel: Den lokale butik sælger 3 slags tærter.
- Æbletærter koster 3$ stykket
- Kirsebærtærter koster 4$ stykket
- Blåbærtærter koster 2$ stykket
Og så mange har de solgt på 4 dage:
Tænk nu over dette … værdien af salget for mandag beregnes på denne måde:
Så det er i virkeligheden “prikproduktet” af priserne og hvor mange der blev solgt:
($3, $4, $2) – (13, 8, 6) = $3×13 + $4×8 + $2×6
= $83
Vi matcher prisen med, hvor mange der er solgt, multiplicerer hver af dem og summerer derefter resultatet.
Med andre ord:
- Salget for mandag var:
- Salget for mandag var: Æbletærter: $3×13=$39, Kirsebærtærter: $4×8=$32, og Blåbærtærter: $2×6=$12. Tilsammen er det 39$ + 32$ + 12$ = 83$
- Og for tirsdag: $3×9 + $4×7 + $2×4 = 63$
- Og for onsdag: $3×7 + $4×4 + $2×0 = 37$
- Og for torsdag: $3×15 + $4×6 + $2×3 = 75$
Så det er vigtigt at tilpasse hver pris til hver mængde.
Nu ved du, hvorfor vi bruger “prikproduktet”.
Og her er det fulde resultat i matrixform:

De solgte tærter for 83 $ om mandagen, 63 $ om tirsdagen, osv.
(Du kan sætte disse værdier ind i matrixberegneren for at se, om de virker.)
Rækker og kolonner
For at vise, hvor mange rækker og kolonner en matrix har, skriver vi ofte rækker×kolonner.
Eksempel: Når vi foretager en multiplikation:
- Tallet af kolonner i den første matrix skal være lig med antallet af rækker i den anden matrix.
- Og resultatet vil have det samme antal rækker som den første matrix og det samme antal kolonner som den anden matrix.
Eksempel:

I dette eksempel har vi ganget en 1×3-matrix med en 3×4-matrix (bemærk, at 3’erne er de samme), og resultatet blev en 1×4-matrix.
I det hele taget:
For at gange en m×n-matrix med en n×p-matrix skal ns’erne være de samme,
og resultatet er en m×p-matrix.
![]()
![]()
Så … ved at gange en 1×3 med en 3×1 får man et 1×1 resultat:
Men ved at gange et 3×1 med et 1×3 får man et 3×3 resultat:
Identitetsmatrix
“Identitetsmatrixen” er den matrix, der svarer til tallet “1”:
En 3×3 identitetsmatrix
- Den er “kvadratisk” (har samme antal rækker som kolonner)
- Den kan være stor eller lille (2×2, 100×100, … uanset hvad)
- Den har 1’er på hoveddiagonalen og 0’er alle andre steder
- Dets symbol er det store bogstav I
Det er en særlig matrix, for når vi multiplicerer med den, er originalen uændret:
A × I = A
I × A = A
Ordning for multiplikation
I aritmetikken er vi vant til:
3 × 5 = 5 × 3
(Den kommutative lov om multiplikation)
Men det gælder generelt ikke for matricer (matrixmultiplikation er ikke kommutativ):
AB ≠ BA
Når vi ændrer rækkefølgen af multiplikationen, er svaret (normalt) anderledes.
Eksempel:
Se, hvordan ændringen af rækkefølgen påvirker denne multiplikation:
Svarene er forskellige!
Det kan give det samme resultat (f.eks. når den ene matrix er identitetsmatrixen), men normalt ikke.




