Eine Matrix ist eine Reihe von Zahlen:

Eine Matrix
(Diese hat 2 Zeilen und 3 Spalten)
Eine Matrix mit einer einzelnen Zahl zu multiplizieren ist einfach:
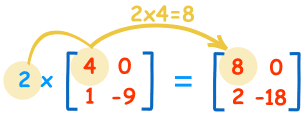
| 2×4=8 | 2×0=0 |
| 2×1=2 | 2×-9=-18 |
Die Zahl (in diesem Fall „2“) nennen wir einen Skalar, deshalb nennt man dies „Skalarmultiplikation“.
Multiplizieren einer Matrix mit einer anderen Matrix
Aber um eine Matrix mit einer anderen Matrix zu multiplizieren, müssen wir das „Punktprodukt“ von Zeilen und Spalten bilden … was bedeutet das? Sehen wir uns das an einem Beispiel an:
Um die Antwort für die 1. Zeile und die 1. Spalte zu berechnen:
Beim „Punktprodukt“ multiplizieren wir übereinstimmende Elemente und addieren dann:
(1, 2, 3) – (7, 9, 11) = 1×7 + 2×9 + 3×11
= 58
Wir gleichen die 1. Glieder (1 und 7) ab, multiplizieren sie, ebenso die 2. Glieder (2 und 9) und die 3. Glieder (3 und 11), und summieren sie schließlich auf.
Wollen Sie ein weiteres Beispiel sehen? Hier ist es für die 1. Zeile und 2. Spalte:
(1, 2, 3) – (8, 10, 12) = 1×8 + 2×10 + 3×12
= 64
Das Gleiche können wir für die 2. Zeile und 1. Spalte machen:
(4, 5, 6) – (7, 9, 11) = 4×7 + 5×9 + 6×11
= 139
Und für die 2. Zeile und 2. Spalte:
(4, 5, 6) – (8, 10, 12) = 4×8 + 5×10 + 6×12
= 154
Und wir erhalten:
FERTIG!
Warum auf diese Weise?
Diese Art zu multiplizieren mag seltsam und kompliziert erscheinen, aber sie ist notwendig!
Ich kann dir ein Beispiel aus dem wirklichen Leben geben, um zu zeigen, warum wir Matrizen auf diese Weise multiplizieren.
Beispiel: Der örtliche Laden verkauft 3 Arten von Kuchen.
- Apfelkuchen kosten 3 $ pro Stück
- Kirschkuchen kosten 4 $ pro Stück
- Blaubeerkuchen kosten 2 $ pro Stück
Und so viele wurden in 4 Tagen verkauft:
Nun überleg mal … der Wert der Verkäufe für Montag wird so berechnet:
So ist es in der Tat das „Punktprodukt“ von Preisen und der Anzahl der verkauften Kuchen:
($3, $4, $2) – (13, 8, 6) = $3×13 + $4×8 + $2×6
= $83
Wir gleichen den Preis mit der Anzahl der verkauften Exemplare ab, multiplizieren beide und addieren dann das Ergebnis.
Mit anderen Worten:
- Die Verkäufe am Montag waren: Apfelkuchen: $3×13=$39, Kirschkuchen: $4×8=$32, und Blaubeerkuchen: $2×6=$12. Zusammen sind das $39 + $32 + $12 = $83
- Und für Dienstag: $3×9 + $4×7 + $2×4 = $63
- Und für Mittwoch: $3×7 + $4×4 + $2×0 = $37
- Und für Donnerstag: $3×15 + $4×6 + $2×3 = $75
Es ist also wichtig, jeden Preis an jede Menge anzupassen.
Nun weißt du, warum wir das „Punktprodukt“ verwenden.
Und hier ist das vollständige Ergebnis in Matrixform:

Am Montag wurden Torten im Wert von 83 Dollar verkauft, am Dienstag 63 Dollar usw.
(Du kannst diese Werte in den Matrix-Rechner eingeben, um zu sehen, ob sie funktionieren.)
Zeilen und Spalten
Um zu zeigen, wie viele Zeilen und Spalten eine Matrix hat, schreiben wir oft Zeilen×Spalten.
Beispiel: Diese Matrix ist 2×3 (2 Zeilen mal 3 Spalten):
Wenn wir multiplizieren:
- Die Anzahl der Spalten der 1. Matrix muss gleich der Anzahl der Zeilen der 2. Matrix sein.
- Und das Ergebnis wird die gleiche Anzahl von Zeilen wie die 1. Matrix und die gleiche Anzahl von Spalten wie die 2. Matrix haben.
Beispiel:

In diesem Beispiel haben wir eine 1×3-Matrix mit einer 3×4-Matrix multipliziert (beachten Sie, dass die 3en gleich sind), und das Ergebnis war eine 1×4-Matrix.
Im Allgemeinen:
Um eine m×n-Matrix mit einer n×p-Matrix zu multiplizieren, müssen die ns gleich sein,
und das Ergebnis ist eine m×p-Matrix.
![]()
So … multipliziert man ein 1×3 mit einem 3×1 erhält man ein 1×1 Ergebnis:
Aber wenn man ein 3×1 mit einem 1×3 multipliziert, erhält man ein 3×3:
Identitätsmatrix
Die „Identitätsmatrix“ ist das Matrixäquivalent der Zahl „1“:
Eine 3×3-Identitätsmatrix
- Sie ist „quadratisch“ (hat die gleiche Anzahl von Zeilen wie Spalten)
- Sie kann groß oder klein sein (2×2, 100×100, … was auch immer)
- Sie hat 1en auf der Hauptdiagonale und 0en überall sonst
- Ihr Symbol ist der Großbuchstabe I
Sie ist eine besondere Matrix, denn wenn wir mit ihr multiplizieren, bleibt das Original unverändert:
A × I = A
I × A = A
Ordnung der Multiplikation
In der Arithmetik sind wir es gewohnt:
3 × 5 = 5 × 3
(Das Kommutativgesetz der Multiplikation)
Aber für Matrizen gilt das im Allgemeinen nicht (die Matrixmultiplikation ist nicht kommutativ):
AB ≠ BA
Wenn wir die Reihenfolge der Multiplikation ändern, ist die Antwort (normalerweise) anders.
Beispiel:
Sieh, wie sich die Änderung der Reihenfolge auf diese Multiplikation auswirkt:
Die Antworten sind unterschiedlich!
Es kann das gleiche Ergebnis haben (z.B. wenn eine Matrix die Identitätsmatrix ist), aber nicht normalerweise.




