Una matriz es una matriz de números:

Una matriz
(Esta tiene 2 filas y 3 columnas)
Multiplicar una matriz por un solo número es fácil:
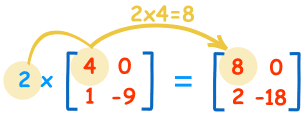
| 2×4=8 | 2×0=0 |
| 2×1=2 | 2×-9=-18 |
Llamamos escalar al número («2» en este caso), por lo que se llama «multiplicación escalar».
Multiplicar una matriz por otra matriz
Pero para multiplicar una matriz por otra matriz tenemos que hacer el «producto punto» de filas y columnas… ¿qué significa eso? Veámoslo con un ejemplo:
Para calcular la respuesta de la 1ª fila y la 1ª columna:
El «producto punto» es cuando multiplicamos los miembros coincidentes y luego sumamos:
(1, 2, 3) – (7, 9, 11) = 1×7 + 2×9 + 3×11
= 58
Emparejamos los primeros miembros (1 y 7), los multiplicamos, al igual que los segundos (2 y 9) y los terceros (3 y 11), y finalmente los sumamos.
¿Quieres ver otro ejemplo? Aquí está para la 1ª fila y 2ª columna:
(1, 2, 3) – (8, 10, 12) = 1×8 + 2×10 + 3×12
= 64
Podemos hacer lo mismo para la 2ª fila y 1ª columna:
(4, 5, 6) – (7, 9, 11) = 4×7 + 5×9 + 6×11
= 139
Y para la 2ª fila y 2ª columna:
(4, 5, 6) – (8, 10, 12) = 4×8 + 5×10 + 6×12
= 154
Y obtenemos:
¡Hecho!
¿Por qué hacerlo así?
Puede parecer una forma extraña y complicada de multiplicar, pero es necesaria!
Puedo poner un ejemplo de la vida real para ilustrar por qué multiplicamos matrices de esta forma.
Ejemplo: La tienda local vende 3 tipos de tartas.
- Las tartas de manzana cuestan 3 dólares cada una
- Las tartas de cereza cuestan 4 dólares cada una
- Las tartas de arándanos cuestan 2 dólares cada una
Y esto es lo que han vendido en 4 días:
Ahora piensa en esto… el valor de las ventas del lunes se calcula así:
Así que es, de hecho, el «producto punto» de los precios y cuántas se vendieron:
($3, $4, $2) – (13, 8, 6) = $3×13 + $4×8 + $2×6
= $83
Coincidimos el precio con cuántos se vendieron, multiplicamos cada uno, y luego sumamos el resultado.
En otras palabras:
- Las ventas del lunes fueron: Tartas de manzana: $3×13=$39, Tartas de cereza: $4×8=$32, y Tartas de arándanos: $2×6=$12. Juntos son 39$ + 32$ + 12$ = 83$
- Y para el martes: 3×9$ + 4×7$ + 2×4$ = 63$
- Y para el miércoles: 3×7$ + 4×4$ + 2×0$ = 37$
- Y para el jueves: 3×15$ + 4×6$ + 2×3$ = 75$
Así que es importante ajustar cada precio a cada cantidad.
Ahora ya sabes por qué usamos el «producto punto».
Y aquí está el resultado completo en forma de matriz:

Se vendieron 83 dólares en pasteles el lunes, 63 dólares el martes, etc.
(Puedes poner esos valores en la calculadora de matrices para ver si funcionan.)
Filas y columnas
Para mostrar cuántas filas y columnas tiene una matriz solemos escribir filas×columnas.
Ejemplo: Esta matriz es de 2×3 (2 filas por 3 columnas):
Cuando hacemos la multiplicación:
- El número de columnas de la 1ª matriz debe ser igual al número de filas de la 2ª matriz.
- Y el resultado tendrá el mismo número de filas que la 1ª matriz, y el mismo número de columnas que la 2ª matriz.
Ejemplo:

En ese ejemplo multiplicamos una matriz de 1×3 por una matriz de 3×4 (nótese que los 3 son iguales), y el resultado fue una matriz de 1×4.
En General:
Para multiplicar una matriz m×n por una matriz n×p, los ns deben ser iguales,
y el resultado es una matriz m×p.
![]()
Entonces… multiplicando un 1×3 por un 3×1 se obtiene un resultado de 1×1:
Pero al multiplicar un 3×1 por un 1×3 se obtiene un resultado de 3×3:
Matriz de Identidad
La «Matriz de Identidad» es la matriz equivalente al número «1»:
Una matriz de identidad 3×3
- Es «cuadrada» (tiene el mismo número de filas que de columnas)
- Puede ser grande o pequeña (2×2, 100×100, … lo que sea)
- Tiene 1s en la diagonal principal y 0s en el resto
- Su símbolo es la letra mayúscula I
Es una matriz especial, porque cuando multiplicamos por ella, el original no cambia:
A × I = A
I × A = A
Orden de multiplicación
En aritmética estamos acostumbrados a:
3 × 5 = 5 × 3
(La ley conmutativa de la multiplicación)
Pero esto no es generalmente cierto para las matrices (la multiplicación matricial no es conmutativa):
AB ≠ BA
Cuando cambiamos el orden de la multiplicación, la respuesta es (normalmente) diferente.
Ejemplo:
Mira cómo afecta el cambio de orden a esta multiplicación:
¡Las respuestas son diferentes!
Puede tener el mismo resultado (como cuando una matriz es la Matriz de Identidad) pero no suele ser así.




