Mikä on ristikko?
Ristikko on järjestetty pistejoukko, joka kuvaa kiteen muodostavien hiukkasten järjestystä.
Kiteen yksikkösolu määritellään ristikkopisteiden avulla.Yksikkösolu on kiteen pienin osa, joka toistettuna säännöllisesti kolmessa ulottuvuudessa tapahtuvan translaation avulla muodostaa koko kiteen.
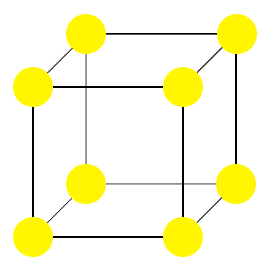
Tässä kuvassa on esimerkiksi primitiivisen kuutiorakenteen yksikkösolu.
Piirretyssä rakenteessa kaikki hiukkaset (keltainen) ovat samoja.
Tässä nimenomaisessa tapauksessa yksikkösolun määrittelevät ristikkopisteet ovat yhteneväiset kiteen hiukkasten keskusten kanssa. Näin ei tarvitse aina olla.
Ioninen ristikko
Jos kide muodostuu ioneista, yhdistettä voidaan kuvata ionisena ristikkona.
Tunnettuja esimerkkejä ionisista hiloista ovat natriumkloridi, kaliumpermanganaatti, booraksi (natriumboraatti) ja kupari(II)sulfaatti.

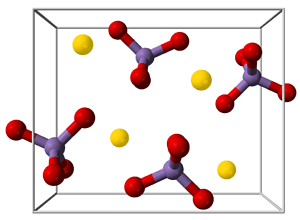
Kovalenttinen ristikko
Jos kide koostuu kovalenttisesti toisiinsa sitoutuneista atomeista, sitä voidaan kuvata kovalenttiseksi ristikoksi tai äärettömäksi kovalenttiseksi ristikoksi.
Tunnettuja esimerkkejä kovalenttisista ristikoista ovat timantti, kvartsi (piidioksidi), pii ja harmaantuminen.
Ristikkovakiot
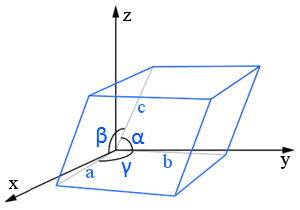
Ristikkovakiot (tai ristikkoparametrit) ovat yksikkösolun reunojen pituudet ja niiden väliset kulmat.
Tässä yhdensuuntaisessa ristikkokaaviossa ristikkovakiot ovat a, b ja c (pituudet) sekä α, β ja γ (kulmat).
Ristikkorakenteet
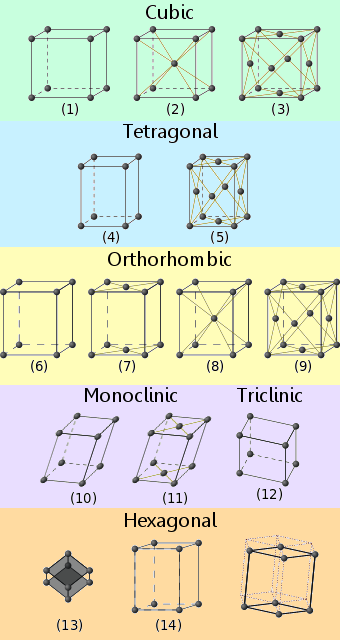
Kiteiset materiaalit sopivat yhteen neljästätoista tunnetusta ristikkojärjestelystä.Näitä kutsutaan Bravais’n ristikoiksi.
Kideverkkojärjestelmien nimet, jotka vastaavat kaavioissa olevia numeroita, ovat seuraavat:
1. Primitiivinen kuutiomainen
2. Runkokeskitetty kuutiomainen
3. Pintakeskitetty kuutiomainen
4. Primitiivinen tetragonaalinen
5. Runkokeskitetty tetragonaalinen
6. Primitiivinen orthorhombinen
7. Pohjakeskitetty orthorhombinen
8. Runkokeskitetty orthorhombinen
9. Pintakeskitetty ortorombinen
10. Alkeellinen monokliininen
11. Pohjakeskitetty monokliininen
12. Trikliininen
13. Romboedrinen
14. Heksagonaalinen
Ristikkovirheet
Jos kiteen oletettaisiin perustuvan matemaattisesti täydelliseen ioniseen ristikkoon, sen laskennallinen vetolujuus olisi paljon suurempi kuin todellisuudessa havaitaan.