Une matrice est un tableau de nombres:

A Matrix
(Celle-ci a 2 rangées et 3 colonnes)
Pour multiplier une matrice par un seul nombre, c’est facile:
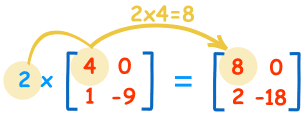
| 2×4=8 | 2×0=0 |
| 2×1=2 | 2×-9=-18 |
On appelle le nombre (« 2 » dans ce cas) un scalaire, on parle donc de « multiplication scalaire ».
Multiplication d’une matrice par une autre matrice
Mais pour multiplier une matrice par une autre matrice, nous devons faire le « produit scalaire » des lignes et des colonnes… qu’est-ce que cela signifie ? Voyons avec un exemple:
Pour calculer la réponse pour la 1ère ligne et la 1ère colonne:
Le « produit scalaire » consiste à multiplier les membres correspondants, puis à faire la somme :
(1, 2, 3) – (7, 9, 11) = 1×7 + 2×9 + 3×11
= 58
Nous faisons correspondre les 1ers membres (1 et 7), nous les multiplions, de même pour les 2èmes membres (2 et 9) et les 3èmes membres (3 et 11), et enfin nous les additionnons.
Vous voulez voir un autre exemple ? Le voici pour la 1ère ligne et la 2ème colonne :
(1, 2, 3) – (8, 10, 12) = 1×8 + 2×10 + 3×12
= 64
Nous pouvons faire la même chose pour la 2ème ligne et la 1ère colonne :
(4, 5, 6) – (7, 9, 11) = 4×7 + 5×9 + 6×11
= 139
Et pour la 2ème ligne et la 2ème colonne :
(4, 5, 6) – (8, 10, 12) = 4×8 + 5×10 + 6×12
= 154
Et on obtient :
Fait !
Pourquoi faire de cette façon?
Cette façon de multiplier peut sembler étrange et compliquée, mais elle est nécessaire!
Je peux vous donner un exemple concret pour illustrer pourquoi nous multiplions les matrices de cette façon.
Exemple : Le magasin local vend 3 types de tartes.
- Les tartes aux pommes coûtent 3 $ chacune
- Les tartes aux cerises coûtent 4 $ chacune
- Les tartes aux myrtilles coûtent 2 $ chacune
Et voici combien ils en ont vendu en 4 jours:
Maintenant pensez à ceci…. la valeur des ventes pour le lundi est calculée de cette façon:
C’est donc, en fait, le « produit scalaire » des prix et de la quantité vendue :
($3, $4, $2) – (13, 8, 6) = $3×13 + $4×8 + $2×6
= $83
Nous faisons correspondre le prix au nombre de vendus, nous multiplions chacun, puis nous additionnons le résultat.
En d’autres termes:
- Les ventes de lundi étaient : Tartes aux pommes : 3×13=39$, Tartes aux cerises : 4×8=32$, et Tartes aux bleuets : 2×6=12$. Ensemble, cela fait 39 $ + 32 $ + 12 $ = 83 $
- Et pour mardi : 3×9 $ + 4×7 $ + 2×4 $ = 63 $
- Et pour mercredi : 3×7 $ + 4×4 $ + 2×0 $ = 37 $
- Et pour jeudi : 3×15 $ + 4×6 $ + 2×3 $ = 75 $
Il est donc important de faire correspondre chaque prix à chaque quantité.
Maintenant vous savez pourquoi nous utilisons le « produit scalaire ».
Et voici le résultat complet sous forme de matrice :

Ils ont vendu 83 $ de tartes le lundi, 63 $ le mardi, etc.
(Vous pouvez mettre ces valeurs dans la calculatrice de matrice pour voir si elles fonctionnent.)
Lignes et colonnes
Pour montrer combien de lignes et de colonnes une matrice a, on écrit souvent lignes×colonnes.
Exemple : Cette matrice est 2×3 (2 lignes par 3 colonnes):
Quand on fait une multiplication:
- Le nombre de colonnes de la 1ère matrice doit être égal au nombre de lignes de la 2ème matrice.
- Et le résultat aura le même nombre de lignes que la 1ère matrice, et le même nombre de colonnes que la 2ème matrice.
Exemple:

Dans cet exemple, nous avons multiplié une matrice 1×3 par une matrice 3×4 (notez que les 3 sont les mêmes), et le résultat était une matrice 1×4.
En général :
Pour multiplier une matrice m×n par une matrice n×p, les ns doivent être les mêmes,
et le résultat est une matrice m×p.
![]()
Donc… multiplier un 1×3 par un 3×1 donne un résultat 1×1 :
Mais en multipliant un 3×1 par un 1×3 on obtient un résultat 3×3 :
Matrice d’identité
La « matrice d’identité » est la matrice équivalente au nombre « 1 » :
Une matrice d’identité 3×3
- Elle est « carrée » (a le même nombre de lignes que de colonnes)
- Elle peut être grande ou petite (2×2, 100×100, … peu importe)
- Elle a des 1 sur la diagonale principale et des 0 partout ailleurs
- Son symbole est la lettre majuscule I
C’est une matrice spéciale, car lorsqu’on la multiplie par elle, l’original reste inchangé :
A × I = A
I × A = A
Ordre de la multiplication
En arithmétique, nous sommes habitués à :
3 × 5 = 5 × 3
(La loi commutative de la multiplication)
Mais ce n’est généralement pas vrai pour les matrices (la multiplication matricielle n’est pas commutative):
AB ≠ BA
Lorsque nous changeons l’ordre de la multiplication, la réponse est (généralement) différente.
Exemple :
Voyez comment le changement d’ordre affecte cette multiplication :
Les réponses sont différentes !
On peut avoir le même résultat (comme lorsqu’une matrice est la matrice d’identité) mais pas habituellement.




