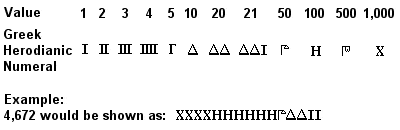
Starożytna grecka Herodianic cyfry
Jak greckie imperium zaczęło rozprzestrzeniać swoją strefę wpływów w Azji Mniejszej, Mezopotamii i dalej, Grecy byli wystarczająco inteligentni, aby przyjąć i zaadaptować użyteczne elementy z podbitych społeczeństw. Dotyczyło to w równym stopniu ich matematyki, jak i wszystkiego innego, a elementy matematyki przejęli zarówno od Babilończyków, jak i Egipcjan. Wkrótce jednak sami zaczęli wnosić istotny wkład i po raz pierwszy możemy uznać wkład pojedynczych osób. Do okresu hellenistycznego Grecy przewodniczyli jednej z najbardziej dramatycznych i ważnych rewolucji w myśli matematycznej wszechczasów.
Liczby attyckie lub herodiańskie
Starożytny grecki system liczbowy, znany jako liczby attyckie lub herodiańskie, był w pełni rozwinięty do około 450 r. p.n.e., a w regularnym użyciu prawdopodobnie już w VII w. p.n.e. Był to system dziesiętny, podobny do systemu liczbowego, który był podobny do systemu dziesiętnego. Był to system bazowy 10 podobny do wcześniejszego egipskiego (a nawet bardziej podobny do późniejszego systemu rzymskiego), z symbolami dla 1, 5, 10, 50, 100, 500 i 1,000 powtórzonymi tyle razy, ile potrzeba do przedstawienia pożądanej liczby. Dodawanie odbywało się poprzez oddzielne sumowanie symboli (1s, 10s, 100s, itd.) w liczbach, które miały być dodane, a mnożenie było pracochłonnym procesem opartym na kolejnych podwojeniach (dzielenie opierało się na odwrotności tego procesu).
Twierdzenie o przechyle Talesa
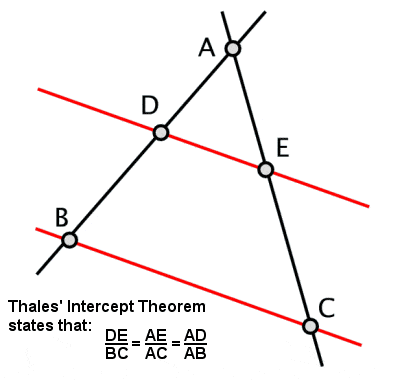
Twierdzenie o przechyle Talesa
Większość greckiej matematyki opierała się jednak na geometrii. Thales, jeden z siedmiu mędrców starożytnej Grecji, który żył na jońskich wybrzeżach Azji Mniejszej w pierwszej połowie VI wieku p.n.e., jest zwykle uważany za pierwszego, który ustanowił wytyczne dla abstrakcyjnego rozwoju geometrii, chociaż to, co wiemy o jego pracy (np. o trójkątach podobnych i prostych) wydaje się teraz dość elementarne.
Thales ustanowił to, co stało się znane jako Twierdzenie Talesa, według którego jeśli trójkąt jest narysowany wewnątrz okręgu z dłuższym bokiem jako średnica okręgu, to przeciwległy kąt zawsze będzie kątem prostym (jak również kilka innych powiązanych właściwości wynikających z tego). Przypisuje mu się również inne twierdzenie, znane również jako twierdzenie Talesa lub twierdzenie o przechwyceniu, o stosunkach odcinków linii, które są tworzone, jeśli dwie przecinające się linie są przechwytywane przez parę równoleżników (i, przez rozszerzenie, stosunki boków podobnych trójkątów).
Do pewnego stopnia, jednak legenda matematyka Pitagorasa z Samos z 6 wieku p.n.e. stała się synonimem narodzin greckiej matematyki. Rzeczywiście, uważa się, że to on ukuł zarówno słowa „filozofia” („miłość do mądrości”), jak i „matematyka” („to, co poznane”). Pitagoras był być może pierwszym, który zdał sobie sprawę, że można skonstruować kompletny system matematyczny, w którym elementy geometryczne odpowiadają liczbom. Twierdzenie Pitagorasa (lub Twierdzenie Pitagorejskie) jest jednym z najbardziej znanych twierdzeń matematycznych. Pozostaje on jednak, jak zobaczymy, postacią kontrowersyjną, a matematyka grecka nie była bynajmniej ograniczona do jednego człowieka.
Trzy problemy geometryczne
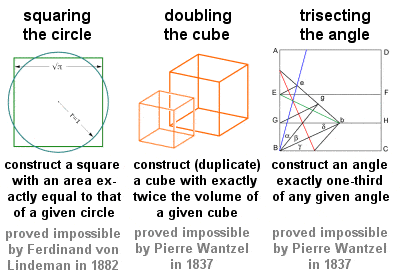
Trzy klasyczne problemy
Trzy problemy geometryczne w szczególności, często nazywane Trzema Klasycznymi Problemami, a wszystkie do rozwiązania środkami czysto geometrycznymi przy użyciu tylko prostej krawędzi i kompasu, pochodzą z wczesnych dni geometrii greckiej: „Kwadratura koła”, „podwojenie (lub powielenie) sześcianu” i „trójkąt kąta”. Te nieprzejednane problemy miały głęboki wpływ na przyszłą geometrię i doprowadziły do wielu owocnych odkryć, chociaż ich rzeczywiste rozwiązania (lub, jak się okazało, dowody ich niemożliwości) musiały czekać aż do XIX w.
Hippokrates z Chios (nie mylić z wielkim greckim lekarzem Hipokratesem z Kos. Szczegółowa biografia tutaj.) był jednym z takich greckich matematyków, który zastosował się do tych problemów w 5 wieku p.n.e. (jego wkład do problemu „kwadratury koła” jest znany jako Lune Hipokratesa). Jego wpływowa książka „Elementy”, datowana na około 440 rok p.n.e., była pierwszą kompilacją elementów geometrii, a jego praca była ważnym źródłem dla późniejszych prac Euklidesa.
Paradoks Achillesa i żółwia
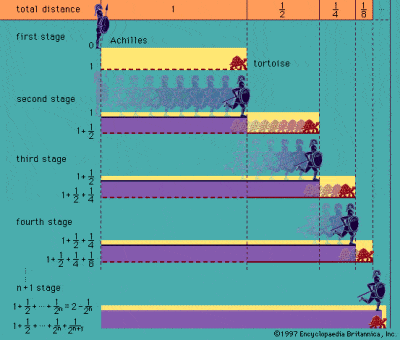
Paradoks Achillesa i żółwia
To Grecy jako pierwsi zmagali się z ideą nieskończoności, opisaną w znanych paradoksach przypisywanych filozofowi Zenonowi z Elei w V wieku p.n.e. Najsłynniejsze z jego paradoksów to te, które zostały opisane w „Księdze tajemnic”. Najsłynniejszym z jego paradoksów jest ten o Achillesie i żółwiu, który opisuje teoretyczny wyścig pomiędzy Achillesem i żółwiem. Achilles daje dużo wolniejszemu żółwiowi przewagę, ale zanim Achilles dotrze do punktu startu żółwia, żółw już rusza do przodu. W czasie, gdy Achilles osiąga ten punkt, żółw ruszył dalej, itd, itp, tak, że w zasadzie szybki Achilles nigdy nie może dogonić powolnego żółwia.
Paradoksy takie jak ten i Zenona tzw. Paradoks Dychotomii opierają się na nieskończonej podzielności przestrzeni i czasu, i opierają się na idei, że połowa plus ćwierć plus ósma plus szesnasta, itd, itd, itd, do nieskończoności nigdy nie będzie całkiem równa całości. Paradoks wynika jednak z fałszywego założenia, że niemożliwe jest wykonanie nieskończonej liczby dyskretnych kresek w skończonym czasie, choć niezwykle trudno jest ostatecznie udowodnić ten fałsz. Starożytny Grek Arystoteles był pierwszym z wielu, który próbował obalić paradoksy, zwłaszcza, że był on zdecydowanym zwolennikiem tego, że nieskończoność może być tylko potencjalna, a nie rzeczywista.
Demokryt, najbardziej znany ze swych proroczych idei o tym, że cała materia składa się z maleńkich atomów, był również pionierem matematyki i geometrii w V-IV wieku p.n.e., i stworzył dzieła o tytułach takich jak „O liczbach”, „O geometrii”, „O stycznych”, „O odwzorowywaniu” i „O irracjach”, chociaż dzieła te nie zachowały się. Wiemy, że był jednym z pierwszych, którzy zauważyli, że stożek (lub ostrosłup) ma jedną trzecią objętości walca (lub graniastosłupa) o tej samej podstawie i wysokości, i jest prawdopodobnie pierwszym, który poważnie rozważał podział obiektów na nieskończoną liczbę przekrojów.
Jednakże z pewnością prawdą jest, że Pitagoras w szczególności wywarł wielki wpływ na tych, którzy przyszli po nim, w tym Platona, który założył swoją słynną Akademię w Atenach w 387 r. p.n.e., i jego protegowanego Arystotelesa, którego praca na temat logiki była uważana za ostateczną przez ponad dwa tysiące lat. Platon matematyk jest najbardziej znany ze swego opisu pięciu brył platońskich, ale wartość jego pracy jako nauczyciela i popularyzatora matematyki jest nie do przecenienia.
Uczeń Platona, Eudoksos z Cnidus, jest zwykle przypisywany pierwszemu wdrożeniu „metody wyczerpania” (rozwiniętej później przez Archimedesa), wczesnej metody całkowania przez kolejne przybliżenia, którą wykorzystał do obliczenia objętości ostrosłupa i stożka. Rozwinął także ogólną teorię proporcji, która miała zastosowanie zarówno do wielkości niewspółmiernych (irracjonalnych), których nie można wyrazić jako stosunku dwóch liczb całkowitych, jak i do wielkości współmiernych (racjonalnych), rozszerzając w ten sposób niepełne idee Pitagorasa.
Prawdopodobnie najważniejszym pojedynczym wkładem Greków, chociaż – i Pitagoras, Platon i Arystoteles byli wszyscy wpływowi w tym względzie – była idea dowodu i dedukcyjna metoda używania logicznych kroków do udowodnienia lub obalenia twierdzeń z początkowo założonych aksjomatów. Starsze kultury, takie jak Egipcjanie i Babilończycy, opierały się na rozumowaniu indukcyjnym, czyli wykorzystywały powtarzane obserwacje do ustalania reguł postępowania. To właśnie koncepcja dowodu nadaje matematyce jej moc i zapewnia, że sprawdzone teorie są tak samo prawdziwe dziś, jak były dwa tysiące lat temu, i która położyła podwaliny pod systematyczne podejście do matematyki Euklidesa i tych, którzy przyszli po nim.
| <<Powrót do matematyki egipskiej | Powrót do Pitagorasa >> |
.