Una matrice è una matrice di numeri:

Una matrice
(Questa ha 2 righe e 3 colonne)
Per moltiplicare una matrice per un singolo numero è facile:
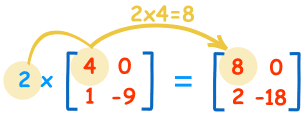
| 2×4=8 | 2×0=0 |
| 2×1=2 | 2×-9=-18 |
Chiamiamo il numero (“2” in questo caso) uno scalare, quindi questa è chiamata “moltiplicazione scalare”.
Moltiplicare una matrice per un’altra matrice
Ma per moltiplicare una matrice per un’altra matrice dobbiamo fare il “prodotto di punti” di righe e colonne… cosa significa? Vediamo con un esempio:
Per calcolare la risposta per la prima riga e la prima colonna:
Il “prodotto a punti” è dove moltiplichiamo i membri corrispondenti, poi sommiamo:
(1, 2, 3) – (7, 9, 11) = 1×7 + 2×9 + 3×11
= 58
Abbiniamo i primi membri (1 e 7), li moltiplichiamo, lo stesso per i secondi (2 e 9) e i terzi (3 e 11), e infine li sommiamo.
Vuoi vedere un altro esempio? Eccolo per la prima riga e la seconda colonna:
(1, 2, 3) – (8, 10, 12) = 1×8 + 2×10 + 3×12
= 64
Possiamo fare la stessa cosa per la seconda riga e la prima colonna:
(4, 5, 6) – (7, 9, 11) = 4×7 + 5×9 + 6×11
= 139
E per la 2a riga e la 2a colonna:
(4, 5, 6) – (8, 10, 12) = 4×8 + 5×10 + 6×12
= 154
E si ottiene:
FATTO!
Perché farlo in questo modo?
Questo può sembrare un modo strano e complicato di moltiplicare, ma è necessario!
Posso darvi un esempio di vita reale per illustrare perché moltiplichiamo le matrici in questo modo.
Esempio: Il negozio locale vende 3 tipi di torte.
- Le torte di mele costano $3 ciascuna
- Le torte di ciliegie costano $4 ciascuna
- Le torte di mirtilli costano $2 ciascuna
E questo è quanto hanno venduto in 4 giorni:
Ora pensate a questo … il valore delle vendite di lunedì è calcolato in questo modo:
Quindi è, in effetti, il “prodotto di punti” dei prezzi e di quante ne sono state vendute:
($3, $4, $2) – (13, 8, 6) = $3×13 + $4×8 + $2×6
= $83
Abbiniamo il prezzo al numero di vendite, moltiplichiamo ciascuno, poi sommiamo il risultato.
In altre parole:
- Le vendite di lunedì sono state: Torte di mele: $3×13=$39, torte di ciliegie: $4×8=$32, e torte di mirtilli: $2×6=$12. Insieme fanno $39 + $32 + $12 = $83
- E per martedì: $3×9 + $4×7 + $2×4 = $63
- E per mercoledì: $3×7 + $4×4 + $2×0 = $37
- E per giovedì: $3×15 + $4×6 + $2×3 = $75
Quindi è importante abbinare ogni prezzo ad ogni quantità.
Ora sai perché usiamo il “prodotto di punti”.
Ecco il risultato completo in forma di matrice:

Hanno venduto 83 dollari di torte lunedì, 63 dollari martedì, ecc.
(Puoi mettere questi valori nella Matrice Calcolatrice per vedere se funzionano.)
Righe e colonne
Per mostrare quante righe e colonne ha una matrice spesso scriviamo righe×colonne.
Esempio: Questa matrice è 2×3 (2 righe per 3 colonne):
Quando facciamo la moltiplicazione:
- Il numero di colonne della prima matrice deve essere uguale al numero di righe della seconda matrice.
- E il risultato avrà lo stesso numero di righe della prima matrice, e lo stesso numero di colonne della seconda matrice.
Esempio:

In quell’esempio abbiamo moltiplicato una matrice 1×3 per una matrice 3×4 (notare che i 3 sono uguali), e il risultato è una matrice 1×4.
In generale:
Per moltiplicare una matrice m×n per una matrice n×p, i n devono essere uguali,
e il risultato è una matrice m×p.
![]()
Quindi … moltiplicando un 1×3 per un 3×1 si ottiene un risultato 1×1:
Ma moltiplicando un 3×1 per un 1×3 si ottiene un risultato 3×3:
Matrice di identità
La “matrice di identità” è la matrice equivalente al numero “1”:
Una matrice di identità 3×3
- È “quadrata” (ha lo stesso numero di righe e colonne)
- Può essere grande o piccola (2×2, 100×100, … qualunque cosa)
- Ha 1 sulla diagonale principale e 0 ovunque
- Il suo simbolo è la lettera maiuscola I
È una matrice speciale, perché quando si moltiplica per essa, l’originale rimane invariato:
A × I = A
I × A = A
Ordine di moltiplicazione
In aritmetica siamo abituati a:
3 × 5 = 5 × 3
(La legge commutativa della moltiplicazione)
Ma questo non è generalmente vero per le matrici (la moltiplicazione delle matrici non è commutativa):
AB ≠ BA
Quando cambiamo l’ordine di moltiplicazione, la risposta è (solitamente) diversa.
Esempio:
Vedi come cambiare l’ordine influenza questa moltiplicazione:
Le risposte sono diverse!
Può avere lo stesso risultato (come quando una matrice è la matrice identità) ma non di solito.




