Metoda Delta-Delta Ct lub metoda Livaka jest najbardziej preferowaną metodą analizy danych qPCR. Jednakże, może być ona stosowana tylko wtedy, gdy spełnione są pewne kryteria. Proszę odnieść się do notatek z wykładu, aby upewnić się, że kryteria te są spełnione. Jeśli nie, bardziej uogólnioną metodą jest metoda Pfaffla. Proszę przeczytać dodatkowe materiały do czytania, aby uzyskać więcej informacji o tej metodzie.
Tutaj są kroki dla metody Livaka:
Plik Excel z wszystkimi obliczeniami są w folderze Analiza qPCR na tablicy.
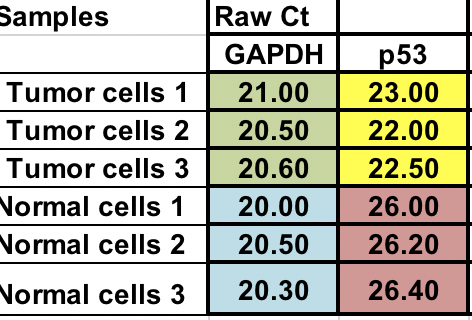
Masz surowe Ct (liczba cykli potrzebna do osiągnięcia progu) dla normalnych i nowotworowych komórek (3 powtórzenia dla każdego).
Normalizacjaś
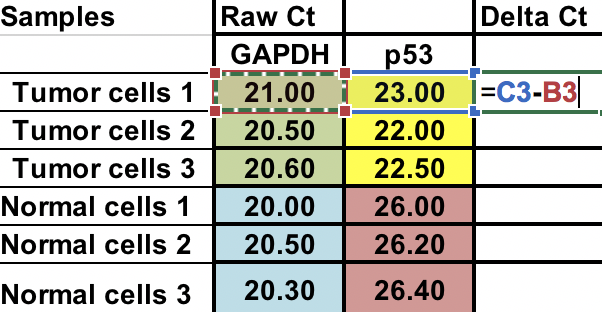
Po pierwsze, będziesz potrzebował obliczyć względną różnicę między genem zainteresowania (p53) i genem domowym (GAPDH).
∆Ct = Ct (gene of interest) – Ct (housekeeping gene)
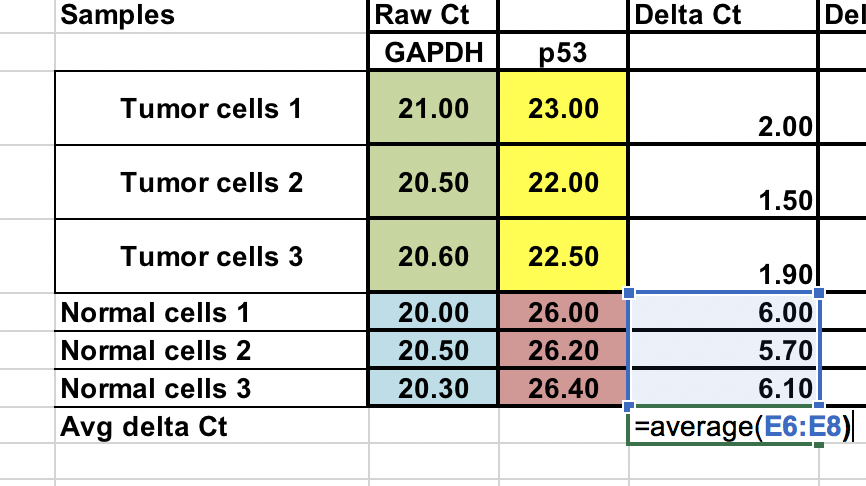
Średnia z próbek kontrolnych (normalnych komórek)Ś
Jak porównamy nasz guz (leczenie) do kontroli (normalnych komórek), najpierw musimy uśrednić ∆Ct dla 3 próbek kontrolnych (normalnych).
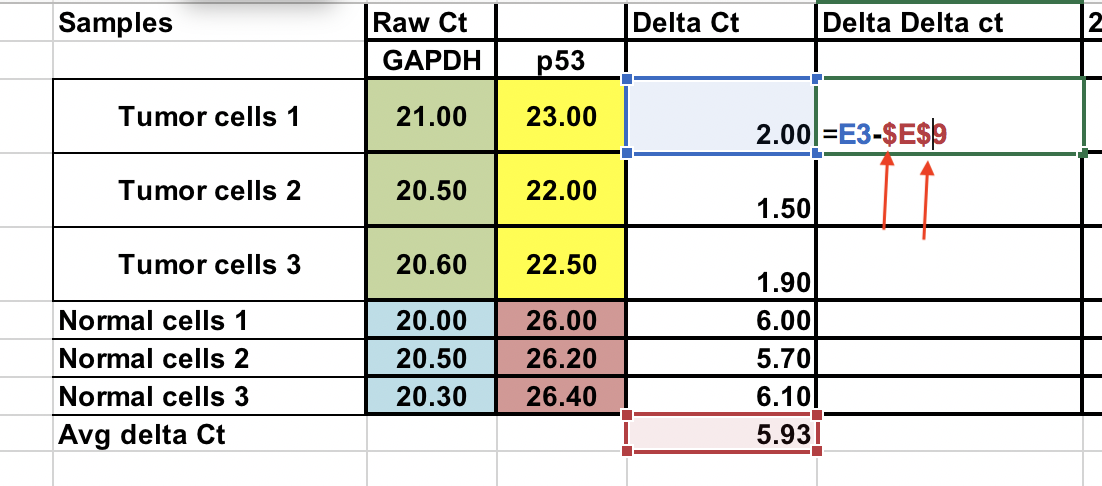
Oblicz ∆∆Ct w stosunku do średniej ∆Ct normalnych komórek komórkiś
∆∆Ct = ∆Ct (próbka guza) – ∆Ct (średnia normalna)
Możesz to zrobić również dla normalnych próbek. Użyj znaków $ przed numerem kolumny i surowej litery (strzałki), aby naprawić komórkę.
Fold ekspresji genów dla każdej próbkiś
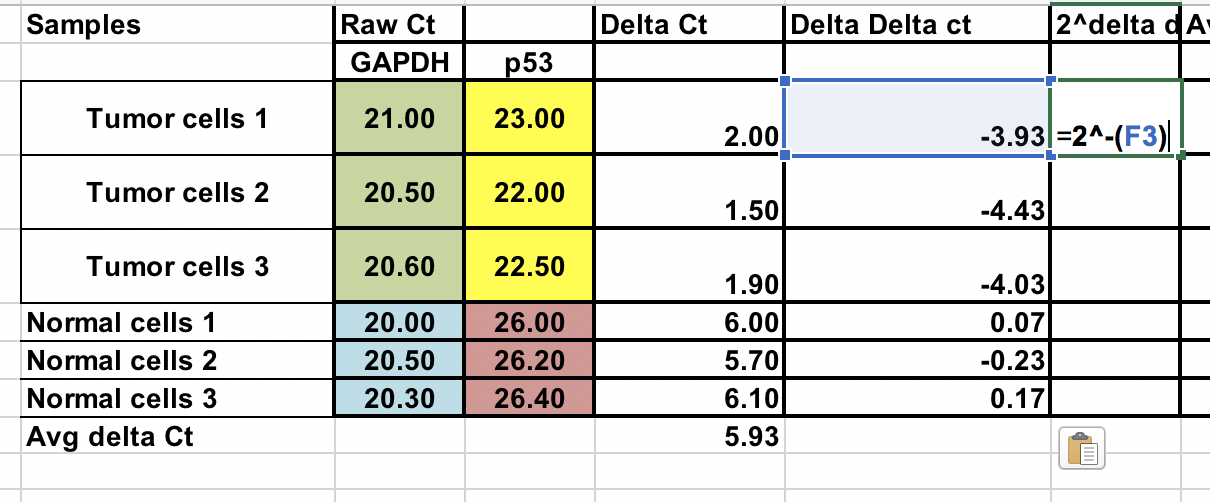
Upewnij się, że podnosisz ujemne ∆∆Ct do potęgi drugiej.
Fold ekspresji genu = 2^-(∆∆Ct)
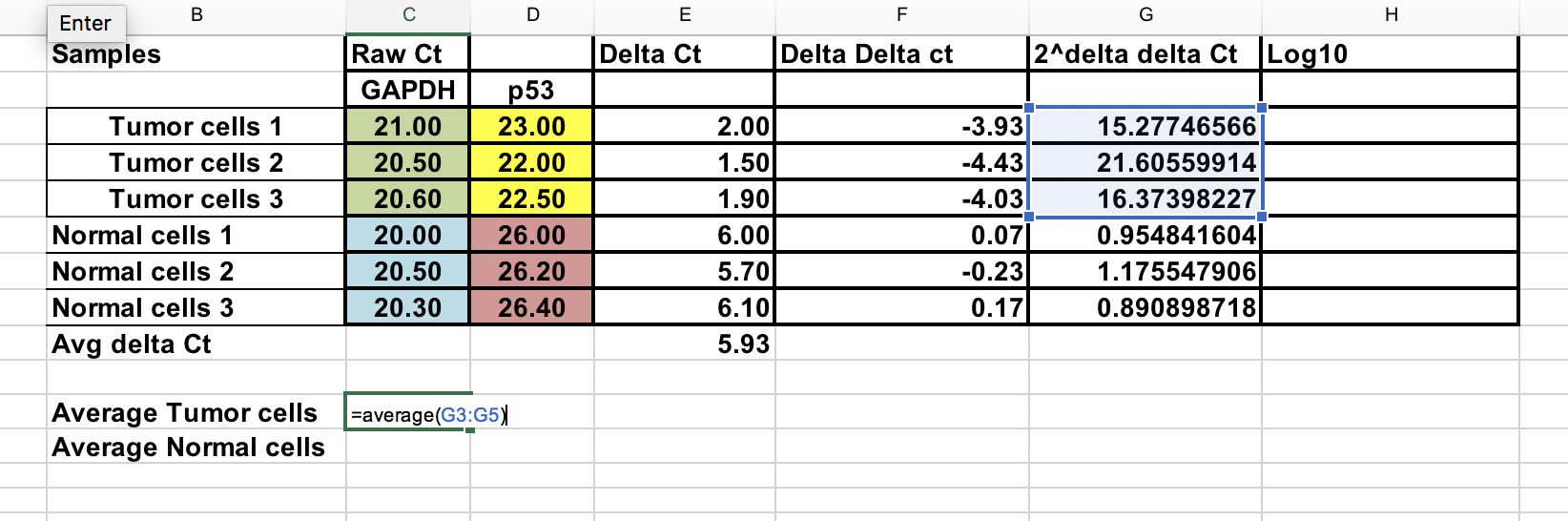
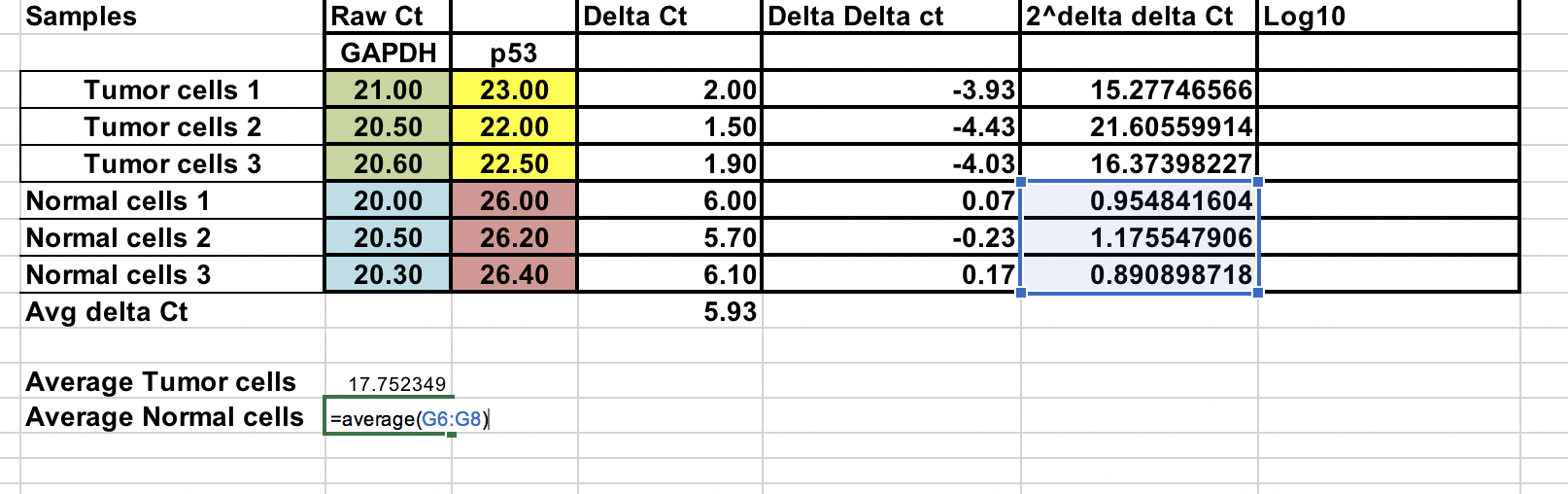
Overall fold changeś
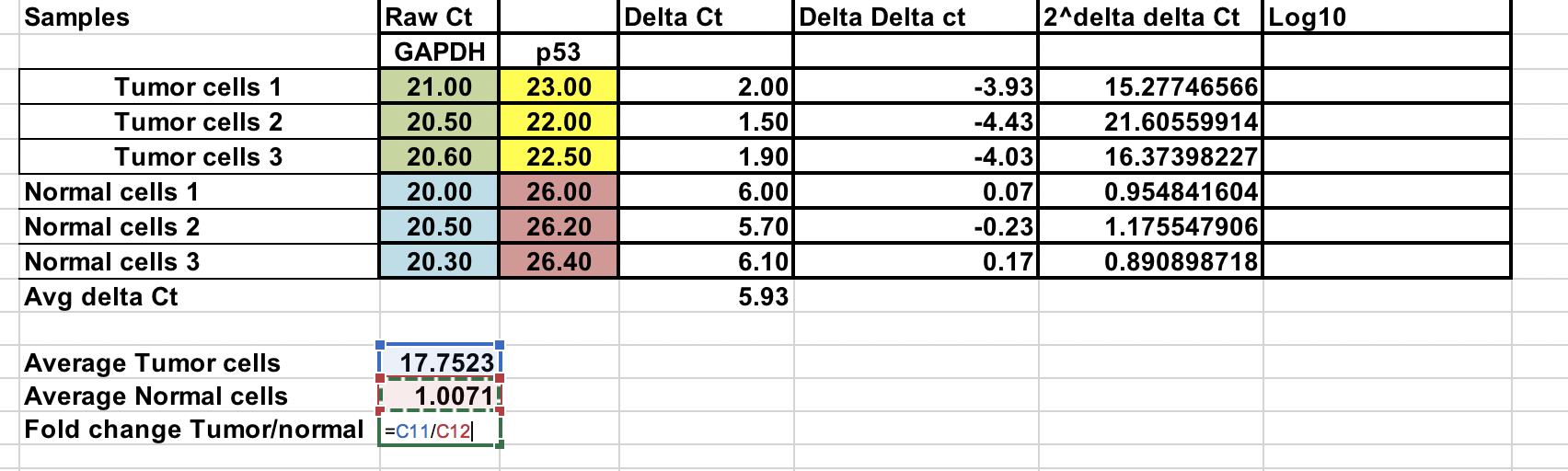
Możesz obliczyć średnią zmianę fold zarówno dla guza jak i normalnych próbek. Stosunek między tymi dwiema wartościami oznacza zmianę fold między próbkami nowotworowymi i prawidłowymi.
Transformacja loguś
Aby wykonać parametryczne testy statystyczne, takie jak test T, zaleca się transformację końcowych wyników ekspresji genów do wartości log (dowolna podstawa log). This would makedata distribution symmetric.
Here we have change the 2^-(∆∆Ct) to log 10.
T-test¶
Need to be careful when using parametric tests if data is not normally distributed, it would lead to erroneous conclusions.
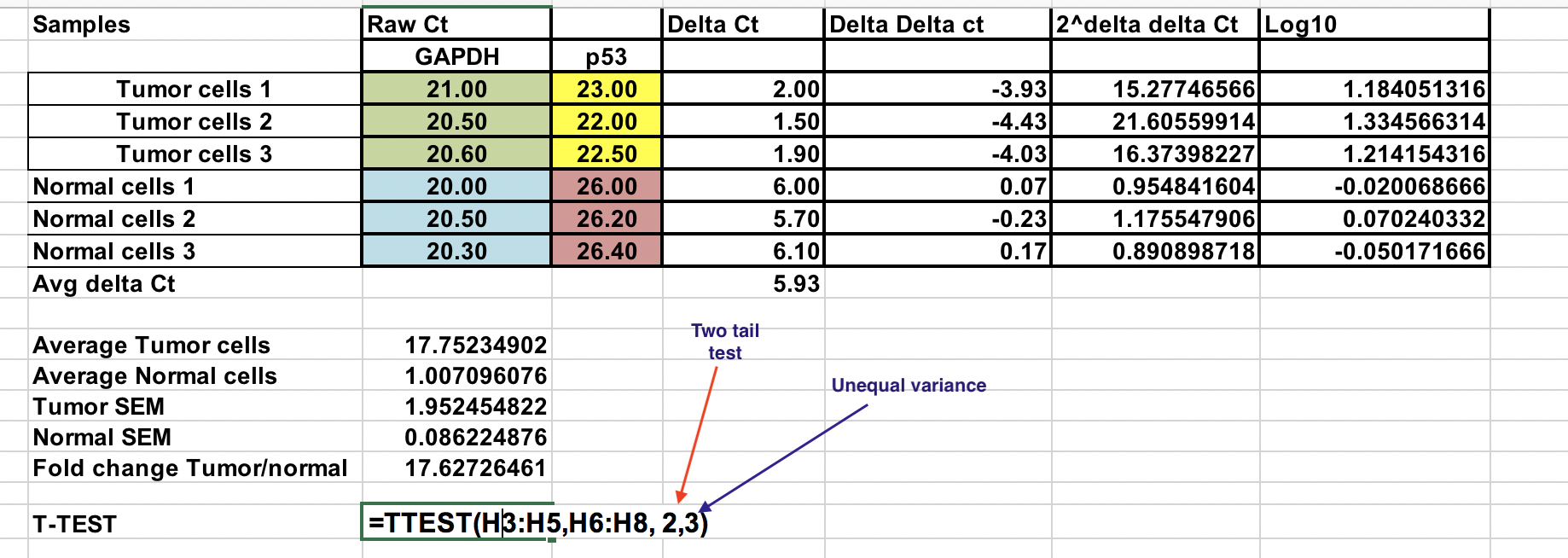
Wybierz log 10 z 2^-(∆∆Ct) wartości dla próbek normalnych i nowotworowych jak wskazano. Użyj testu dwóch ogonów (numer 2) i zakładając nierówną wariancję (3).
Wynik P jest mniejszy niż 0.05 i dlatego odrzucamy hipotezę zerową i dwie średnie z próbek różnią się istotnie na poziomie 0.05.
.