Uma Matriz é uma matriz de números:

Uma Matriz
(Esta tem 2 Linhas e 3 Colunas)
Multiplicar uma matriz por um único número é fácil:
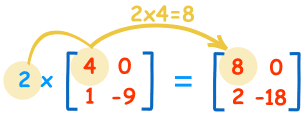
| 2×4=8 | 2×0=0 |
| 2×1=2 | 2×-9=-18 |
Chamamos ao número (“2” neste caso) um escalar, por isso chamamos a isto “multiplicação escalar”.
Multiplicando uma Matriz por Outra Matriz
Mas para multiplicar uma matriz por outra matriz precisamos fazer o “produto ponto” de linhas e colunas … o que isso significa? Vejamos com um exemplo:
Para chegar à resposta para a 1ª linha e 1ª coluna:
O “Dot Product” é onde multiplicamos os membros correspondentes, depois somamos:
(1, 2, 3) – (7, 9, 11) = 1×7 + 2×9 + 3×11
= 58
Funcionamos os primeiros membros (1 e 7), multiplicamo-los, da mesma forma para os segundos membros (2 e 9) e para os terceiros membros (3 e 11), e finalmente somamo-los.
Queres ver outro exemplo? Aqui é para a 1ª linha e 2ª coluna:
(1, 2, 3) – (8, 10, 12) = 1×8 + 2×10 + 3×12
= 64
Podemos fazer o mesmo para a 2ª linha e 1ª coluna:
(4, 5, 6) – (7, 9, 11) = 4×7 + 5×9 + 6×11
= 139
> E para a 2ª fila e 2ª coluna:
(4, 5, 6) – (8, 10, 12) = 4×8 + 5×10 + 6×12
= 154
>E obtemos:
DONE!
Porquê fazer desta forma?
Esta pode parecer uma forma estranha e complicada de multiplicação, mas é necessária!
Posso dar-lhe um exemplo da vida real para ilustrar porque multiplicamos as matrizes desta forma.
Exemplo: A loja local vende 3 tipos de tortas.
- Tortas de maçã custam $3 cada
- Tortas de xerez custam $4 cada
- Tortas de amoreira custam $2 cada
E este é o número que venderam em 4 dias:

Agora pense nisto… o valor das vendas de segunda-feira é calculado desta forma:
Então é, na verdade, o “produto ponto” dos preços e quantos foram vendidos:
($3, $4, $2) – (13, 8, 6) = $3×13 + $4×8 + $2×6
= $83
Coordenamos o preço com quantos foram vendidos, multiplicamos cada um, e depois somamos o resultado.
Em outras palavras:
- As vendas de segunda-feira foram: Tartes de maçã: $3×13=$39, tartes de cereja: $4×8=$32, e tartes de mirtilo: $2×6=$12. Juntos são $39 + $32 + $12 = $83
- E para terça-feira: $3×9 + $4×7 + $2×4 = $63
- >E para quarta-feira: $3×7 + $4×4 + $2×0 = $37
- E para quinta-feira: $3×15 + $4×6 + $2×3 = $75
Por isso é importante fazer corresponder cada preço a cada quantidade.
Agora você sabe porque nós usamos o “produto ponto”.
E aqui está o resultado completo em forma de Matrix:

Venderam tortas no valor de $83 na segunda-feira, $63 na terça-feira, etc.
(Você pode colocar esses valores na Calculadora Matriz para ver se eles funcionam.)
Linhas e Colunas
Para mostrar quantas linhas e colunas uma matriz tem, nós frequentemente escrevemos linhas×colunas.
Exemplo: Esta matriz é 2×3 (2 linhas por 3 colunas):
Quando fazemos multiplicação:
- O número de colunas da 1ª matriz deve ser igual ao número de linhas da 2ª matriz.
- E o resultado terá o mesmo número de linhas da 1ª matriz, e o mesmo número de colunas da 2ª matriz.
Exemplo:

Nesse exemplo multiplicamos uma matriz 1×3 por uma matriz 3×4 (note que os 3s são os mesmos), e o resultado foi uma matriz 1×4.
Em Geral:
Para multiplicar uma matriz m×n por uma matriz n×p, os ns devem ser os mesmos,
e o resultado é uma matriz m×p.
![]()
Então … multiplicando um 1×3 por um 3×1 obtém-se um resultado 1×1:
>
Mas a multiplicação de 3×1 por 1×3 obtém um resultado 3×3:
Matriz da Identidade
A “Matriz da Identidade” é a matriz equivalente ao número “1”:
A Matriz de Identidade 3×3
- É “quadrada” (tem o mesmo número de linhas das colunas)
- Pode ser grande ou pequena (2×2, 100×100, … o que quer que seja)
- Tem 1s na diagonal principal e 0s em todo o lado
- Its símbolo é a letra maiúscula I
É uma matriz especial, porque quando nos multiplicamos por ela, o original permanece inalterado:
A × I = A
I × A = A
Ordem de multiplicação
Em aritmética estamos acostumados:
3 × 5 = 5 × 3
(A Lei Comutativa da Multiplicação)
Mas isto não é geralmente verdade para matrizes (a multiplicação matricial não é comutativa):
AB ≠ BA
Quando mudamos a ordem da multiplicação, a resposta é (geralmente) diferente.
Exemplo:
Ver como a alteração da ordem afecta esta multiplicação:
>
>>
As respostas são diferentes!
Pode ter o mesmo resultado (tal como quando uma matriz é a Matriz de Identidade) mas não normalmente.



