O matrice este o matrice de numere:

O matrice
(Aceasta are 2 rânduri și 3 coloane)
Pentru a înmulți o matrice cu un singur număr este ușor:
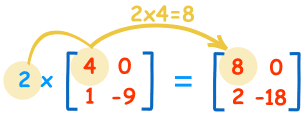
| 2×4=8 | 2×0=0 |
| 2×1=2 | 2×-9=-18 |
Noi numim numărul („2” în acest caz) un scalar, astfel încât acest lucru se numește „înmulțire scalară”.
Înmulțirea unei matrice cu o altă matrice
Dar pentru a înmulți o matrice cu o altă matrice trebuie să facem „produsul punctat” al rândurilor și coloanelor … ce înseamnă asta? Să vedem cu un exemplu:
Pentru a calcula răspunsul pentru primul rând și prima coloană:
„Produsul punctat” este atunci când înmulțim membrii corespondenți, apoi adunăm:
(1, 2, 3) – (7, 9, 11) = 1×7 + 2×9 + 3×11
= 58
Potrivim primii membri (1 și 7), îi înmulțim, la fel pentru al 2-lea membru (2 și 9) și al 3-lea membru (3 și 11), iar în final îi însumăm.
Vreți să vedeți un alt exemplu? Iată-l pentru rândul 1 și coloana a 2-a:
(1, 2, 3) – (8, 10, 12) = 1×8 + 2×10 + 3×12
= 64
Potem face același lucru pentru rândul 2 și coloana 1:
(4, 5, 6) – (7, 9, 11) = 4×7 + 5×9 + 6×11
= 139
Și pentru al 2-lea rând și a 2-a coloană:
(4, 5, 6) – (8, 10, 12) = 4×8 + 5×10 + 6×12
= 154
Și obținem:
FĂCUT!
De ce să procedăm astfel?
Acesta poate părea un mod ciudat și complicat de înmulțire, dar este necesar!
Vă pot da un exemplu din viața reală pentru a ilustra de ce înmulțim matricile în acest mod.
Exemplu: Magazinul local vinde 3 tipuri de plăcinte.
- Plăcintele cu mere costă 3 dolari bucata
- Plăcintele cu cireșe costă 4 dolari bucata
- Plăcintele cu afine costă 2 dolari bucata
Și iată câte au vândut în 4 zile:
Acum gândiți-vă la asta … valoarea vânzărilor pentru ziua de luni se calculează astfel:
Așa că este, de fapt, „produsul în puncte” dintre prețuri și câte s-au vândut:
(3$, 4$, 2$) – (13, 8, 6) = 3×13$ + 4×8$ + 2×6$
= 83$
Se potrivește prețul cu numărul de exemplare vândute, se înmulțește fiecare, apoi se însumează rezultatul.
Cu alte cuvinte:
- Vânzările pentru luni au fost: Plăcinte cu mere: 3×13=39$, Plăcinte cu cireșe: 4×8=32$ și Plăcinte cu afine: 2×6=12$. Împreună înseamnă 39$ + 32$ + 12$ = 83$
- Și pentru marți: 3$×9$ + 4$×7$ + 2$×4$ = 63$
- Și pentru miercuri: 3$×7$ + 4$×4$ + 2$×0$ = 37$
- Și pentru joi: 3$×15$ + 4$×6$ + 2$×3$ = 75$
Deci este important să se potrivească fiecare preț cu fiecare cantitate.
Acum știți de ce folosim „produsul cu puncte”.
Și iată rezultatul complet sub formă de matrice:

Au vândut plăcinte în valoare de 83 de dolari luni, 63 de dolari marți, etc.
(Puteți introduce aceste valori în Matrix Calculator pentru a vedea dacă funcționează.)
Rânduri și coloane
Pentru a arăta câte rânduri și câte coloane are o matrice, scriem adesea rânduri×coloane.
Exemplu: Această matrice este 2×3 (2 rânduri pe 3 coloane):
Când facem înmulțirea:
- Numărul de coloane din prima matrice trebuie să fie egal cu numărul de rânduri din cea de-a doua matrice.
- Și rezultatul va avea același număr de rânduri ca și prima matrice și același număr de coloane ca și cea de-a doua matrice.
Exemplu:

În acest exemplu am înmulțit o matrice 1×3 cu o matrice 3×4 (observați că 3-urile sunt aceleași), iar rezultatul a fost o matrice 1×4.
În general:
Pentru a înmulți o matrice m×n cu o matrice n×p, ns trebuie să fie aceiași,
și rezultatul este o matrice m×p.
![]()
Atunci … înmulțind un 1×3 cu un 3×1 se obține un rezultat 1×1:
Dar înmulțind un 3×1 cu un 1×3 se obține un rezultat 3×3:
Matrice de identitate
„Matricea de identitate” este echivalentul matricial al numărului „1”:
O matrice de identitate 3×3
- Este „pătrată” (are același număr de rânduri și de coloane)
- Poate fi mare sau mică (2×2, 100×100, … whatever)
- Are 1-uri pe diagonala principală și 0-uri peste tot în rest
- Simbolul ei este litera majusculă I
Este o matrice specială, deoarece atunci când o înmulțim cu ea, originalul rămâne neschimbat:
A × I = A
I × A = A
Ordinea înmulțirii
În aritmetică suntem obișnuiți:
3 × 5 = 5 × 3
(Legea comutativă a înmulțirii)
Dar acest lucru nu este în general valabil pentru matrici (înmulțirea matricelor nu este comutativă):
AB ≠ BA
Când schimbăm ordinea înmulțirii, răspunsul este (de obicei) diferit.
Exemplu:
Vezi cum afectează schimbarea ordinii această înmulțire:
Răspunsurile sunt diferite!
Se poate obține același rezultat (cum ar fi atunci când o matrice este matricea identitate), dar nu de obicei.




