16.3 Strategie mieszane
Cel nauczania
- Jakie gry wymagają lub dopuszczają losowość jako część swojego rozwiązania?
Rozważmy ponownie grę w dobieranie grosików, jak pokazano na Rysunku 16.13 „Znowu dobieranie groszy”.
Rysunek 16.13 Znowu dobieranie groszy
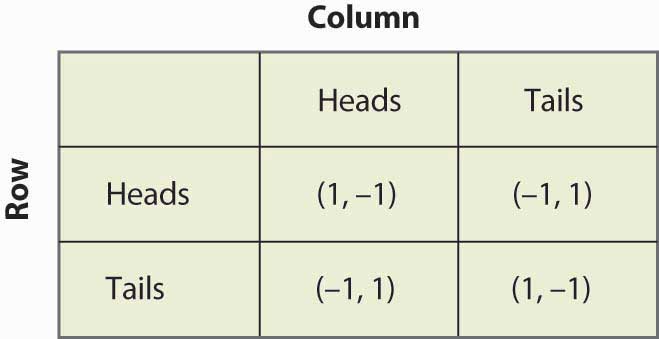
Załóżmy, że Wiersz wierzy, że Kolumna gra w Głowy z prawdopodobieństwem p. Wtedy, jeśli Wiersz gra w Głowy, Wiersz dostaje 1 z prawdopodobieństwem p i -1 z prawdopodobieństwem (1 – p), dla wartości oczekiwanej 2p – 1. Podobnie, jeśli rząd gra w ogon, to otrzymuje -1 z prawdopodobieństwem p (gdy kolumna gra w głowy) oraz 1 z prawdopodobieństwem (1 – p), co daje wartość oczekiwaną 1 – 2p. Podsumowaniem tego jest rysunek 16.14 „Strategia mieszana w dobieraniu groszy”.
Jeśli 2p – 1 > 1 – 2p, to przeciętnie lepiej jest, gdy Wiersz gra Głowy niż Ogony. Podobnie, jeśli 2p – 1 < 1 – 2p, to Rzędowi lepiej jest grać Reszki niż Główki. Jeśli natomiast 2p – 1 = 1 – 2p, to bez względu na to, co zrobi Wiersz, otrzyma taką samą wypłatę. W tym przypadku Row może zagrać Orzeł, może zagrać Reszka lub może rzucić monetą i randomizować zagranie Row.
Równowaga Nasha o mieszanej strategiiRównowaga Nasha, w której co najmniej jeden gracz gra strategię losową i żaden z graczy nie jest w stanie zwiększyć swojej oczekiwanej wypłaty grając strategię alternatywną. polega na tym, że co najmniej jeden gracz gra strategię losową i żaden z graczy nie jest w stanie zwiększyć swojej oczekiwanej wypłaty grając strategię alternatywną. Równowaga Nasha, w której żaden z graczy nie randomizuje nazywana jest czystą strategią Nash equilibrium Równowaga Nasha, w której żaden z graczy nie randomizuje..
Rysunek 16.14 Strategia mieszana w dobieraniu groszy
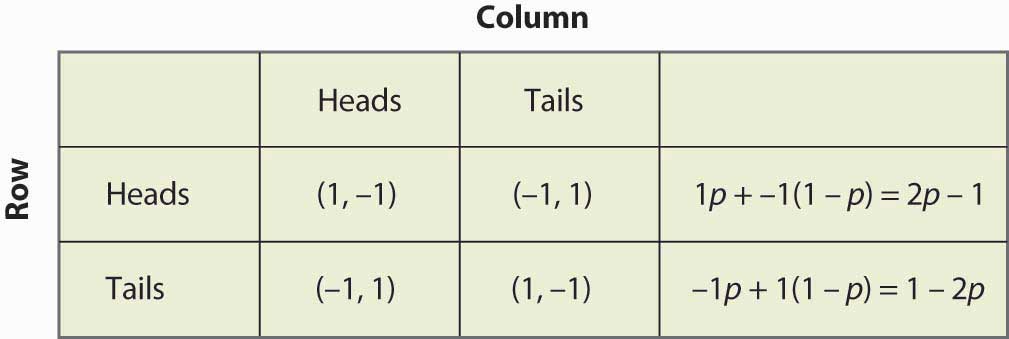
Zauważmy, że randomizacja wymaga równości oczekiwanych wypłat. Jeśli gracz ma losować strategię A lub strategię B, to obie te strategie muszą dawać taką samą oczekiwaną wypłatę. W przeciwnym razie gracz wolałby jedną z nich i nie grałby drugą.
Obliczanie strategii mieszanej ma jeden element, który często wydaje się mylący. Załóżmy, że Row będzie losował. W takim razie wypłata wiersza musi być równa dla wszystkich strategii, które wiersz gra z dodatnim prawdopodobieństwem. Ale ta równość w wypłatach wiersza nie określa prawdopodobieństwa, z jakim wiersz gra różnymi strategiami. Zamiast tego, równość w wypłatach wiersza określa prawdopodobieństwo, z jakim kolumna gra poszczególne kolumny. Powodem tego jest to, że to prawdopodobieństwa kolumn określają oczekiwaną wypłatę dla wiersza; jeśli wiersz będzie losowy, to prawdopodobieństwa kolumn muszą być takie, aby wiersz był skłonny do losowości.
Tak więc, na przykład, obliczyliśmy wypłatę dla wiersza za zagranie głowy, która wynosiła 2p – 1, gdzie p było prawdopodobieństwem, że kolumna zagrała głowę. Analogicznie, wypłata dla Wiersza za zagranie Ogona wynosi 1 – 2p. Wiersz jest skłonny do randomizacji, jeśli te prawdopodobieństwa są równe, co rozwiązuje się dla p = ½.
Spróbujmy teraz nieco trudniejszego przykładu i powróćmy do walki płci. Rysunek 16.15 „Strategia mieszana w bitwie płci” ilustruje jeszcze raz wypłaty.
Rysunek 16.15 Strategia mieszana w bitwie płci
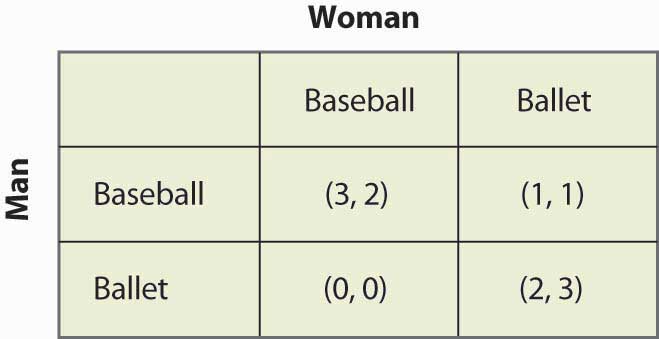
Gra ta ma dwa czyste strategiczne równouprawnienia Nasha: (Baseball, Baseball) i (Balet, Balet). Czy istnieje strategia mieszana? Aby obliczyć strategię mieszaną, niech kobieta pójdzie do gry w baseball z prawdopodobieństwem p, a mężczyzna do gry w baseball z prawdopodobieństwem q. Rysunek 16.16 „Pełne obliczenie strategii mieszanej” zawiera obliczenie wypłat strategii mieszanej dla każdego gracza.
Rysunek 16.16 Pełne obliczenie strategii mieszanej
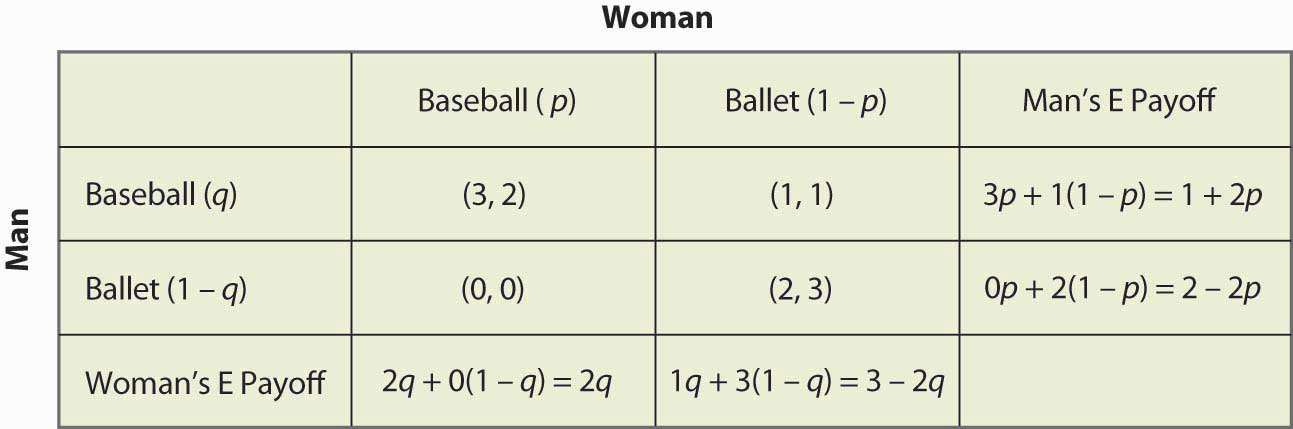
Na przykład, jeśli Mężczyzna (gracz w rzędzie) pójdzie na mecz baseballu, dostanie 3, gdy Kobieta pójdzie na mecz baseballu (prawdopodobieństwo p), a w przeciwnym razie dostanie 1, dla oczekiwanej wypłaty 3p + 1(1 – p) = 1 + 2p. Pozostałe obliczenia są podobne, ale zdecydowanie powinieneś przeprowadzić przez logikę i zweryfikować każde obliczenie.
Strategia mieszana w grze battle of the sexes wymaga, aby obie strony dokonały randomizacji (ponieważ czysta strategia jednej ze stron uniemożliwia randomizację drugiej). Obojętność mężczyzny pomiędzy pójściem na mecz baseballu i na balet wymaga 1 + 2p = 2 – 2p, co daje p = ¼. Oznacza to, że mężczyzna będzie skłonny do losowego wyboru wydarzenia, w którym będzie uczestniczył, jeśli kobieta będzie chodziła na balet ¾ czasu, a w przeciwnym razie na mecz baseballowy. To sprawia, że mężczyźnie jest obojętne, na które z tych dwóch wydarzeń pójdzie, ponieważ woli być z kobietą, ale lubi też być na meczu baseballowym. Aby zrekompensować przewagę, jaką daje mu gra, Kobieta musi częściej bywać na Balecie.
Podobnie, aby Kobieta dokonała randomizacji, musi otrzymać równe wypłaty z pójścia na mecz Baseballu i na Balet, co wymaga 2q = 3 – 2q, czyli q = ¾. Zatem prawdopodobieństwo, że mężczyzna pójdzie na mecz baseballowy wynosi ¾, a na balet pójdzie ¼ czasu. Są to niezależne prawdopodobieństwa, więc aby otrzymać prawdopodobieństwo, że obaj pójdą na mecz baseballowy, mnożymy te prawdopodobieństwa, co daje 3/16. Rysunek 16.17 „Prawdopodobieństwa strategii mieszanej” wypełnia prawdopodobieństwa dla wszystkich czterech możliwych wyników.
Rysunek 16.17 Prawdopodobieństwa strategii mieszanej
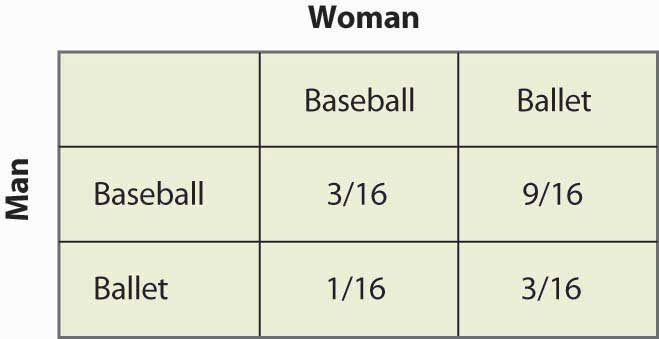
Zauważ, że więcej niż połowa przypadków (Baseball, Balet) jest wynikiem strategii mieszanej i dwie osoby nie są razem. Ten brak koordynacji jest generalnie cechą równowag strategii mieszanych. Oczekiwane wypłaty dla obu graczy są również łatwe do obliczenia. Wypłata mężczyzny wynosi 1 + 2p = 2 – 2p, a ponieważ p = ¼, mężczyzna otrzymuje 1½. Podobna kalkulacja pokazuje, że wypłata kobiety jest taka sama. Zatem oboje radzą sobie gorzej niż koordynując swoje mniej preferowane wyniki. Ale ten mieszana strategia Nash równowaga, niepożądany jak ono może wydawać się, jest Nash równowaga w ten sposób, że żadny strona może ulepszyć jego lub jej swój payoff, dawać zachowanie inny strona.
W bitwie płci, mieszana strategia Nash równowaga może wydawać się nieprawdopodobny; i my móc oczekiwać para skuteczniejszy koordynować. Rzeczywiście, zwykła rozmowa telefoniczna powinna wykluczyć strategię mieszaną. Rozważmy więc inną grę związaną z walką płci, w której brak koordynacji ma więcej sensu. Jest to gra w „kurczaka”. W tej grze dwóch graczy jedzie do siebie nawzajem, próbując przekonać drugiego, by się poddał i ostatecznie zjechał do rowu. Jeśli obaj wjadą do rowu, wynik nazywamy remisem i obaj dostają zero. Jeśli jeden skręca, a drugi nie, kierowca, który skręca przegrywa, a drugi wygrywa i przyznajemy zwycięzcy jeden punkt.Zauważ, że dodanie stałej do wypłaty gracza, lub pomnożenie wypłaty gracza przez dodatnią stałą, nie ma wpływu na równowagę Nasha – czystą lub mieszaną. Dlatego zawsze możemy pozwolić, aby jeden wynik dla każdego gracza wynosił zero, a drugi jeden. Pozostaje tylko pytanie, co się stanie, gdy żaden z graczy nie osiągnie wyniku, w którym to przypadku nastąpi krach. W tej wersji wypłata została ustalona na poziomie czterokrotności straty wynikającej ze zmiany kierunku jazdy, jak pokazano na rysunku 16.18 „Kurczak”, ale możesz zmienić grę i zobaczyć, co się stanie.
Rysunek 16.18 Kurczak
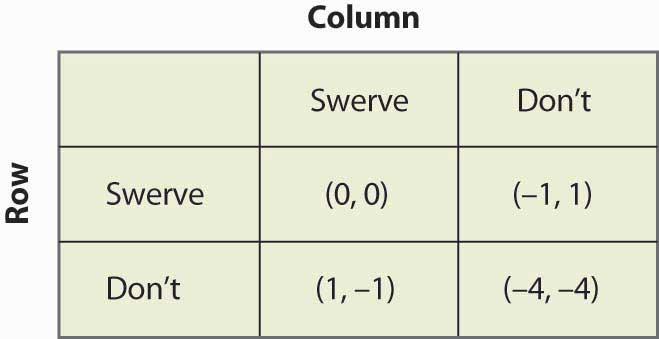
Ta gra ma dwa równania czystej strategii: (Swerve, Don’t) i (Don’t, Swerve). Dodatkowo, gra ma strategię mieszaną. Załóżmy, że Kolumna zachowuje się niestosownie z prawdopodobieństwem p. Wtedy Wiersz dostaje 0p + -1(1 – p) ze zmiany kierunku, 1p + (-4)(1 – p) z braku zmiany kierunku, a Wiersz będzie losował, jeśli te wartości są równe, co wymaga p = ¾. Oznacza to, że w równowadze strategii mieszanej prawdopodobieństwo, że kolumna zmieni kierunek jest równe ¾. Można sprawdzić, że gracz rzędowy ma takie samo prawdopodobieństwo, ustawiając prawdopodobieństwo, że kolumna się uchyla równe q i obliczając oczekiwaną wypłatę kolumny. Tak więc, prawdopodobieństwo kolizji jest 1/16 w równowadze strategii mieszanej.
Równowaga strategii mieszanej jest bardziej prawdopodobna, w pewnym sensie, w tej grze: Jeśli gracze już wiedzieli, kto będzie poddawać się, nie musieliby właściwie grać w grę. Cały sens gry polega na tym, aby dowiedzieć się, kto się podda, co oznacza, że nie jest to z góry wiadome. Oznacza to, że równowaga strategii mieszanej jest, w pewnym sensie, bardziej rozsądną równowagą.
Rysunek 16.19 Kamień, papier, nożyce
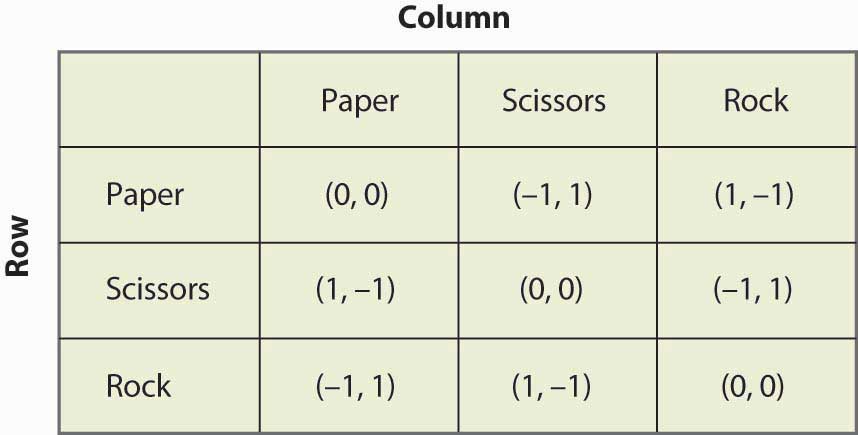
„Kamień, papier, nożyce” jest grą dziecięcą, w której dwoje dzieci używa swoich rąk, aby jednocześnie wybrać papier (ręka trzymana płasko), nożyce (ręka z dwoma palcami wystającymi tak, aby wyglądały jak nożyczki) lub kamień (ręka w pięści). Charakter wygranej polega na tym, że papier bije kamień, kamień bije nożyczki, a nożyczki biją papier. Ta gra ma strukturę przedstawioną na rysunku 16.19 „Kamień, papier, nożyce”.
Kluczowe wnioski
- Równowaga Nasha o mieszanej strategii polega na tym, że co najmniej jeden gracz gra strategię losową i żaden z graczy nie jest w stanie zwiększyć swojej oczekiwanej wypłaty, grając strategię alternatywną.
- Równowaga Nasha bez randomizacji jest nazywana równowagą Nasha o czystej strategii.
- Jeśli gracz ma losowo wybierać dwie strategie, to obie muszą dawać taką samą oczekiwaną wypłatę.
- Gra w dobieranie groszy ma strategię mieszaną i nie ma strategii czystej.
- Gra w bitwę płci ma strategię mieszaną i dwie strategie czyste.
- Gra w kurczaka jest podobna do gry w bitwę płci i tak jak ona ma dwie strategie czyste i jedną mieszaną.
Ćwiczenia
- Pozwól q być prawdopodobieństwem, że Wiersz gra głową. Pokaż, że Kolumna jest skłonna do randomizacji wtedy i tylko wtedy, gdy q = ½. (Wskazówka: najpierw oblicz oczekiwaną wypłatę Kolumny, gdy Kolumna gra Głową, a następnie oblicz oczekiwaną wypłatę Kolumny, gdy Kolumna gra Ogonem. Te wartości muszą być równe, aby Kolumna mogła losowo zagrać.)
- Wykaż, że w grze w kamień, papier, nożyce nie ma równowag czystej strategii. Pokaż, że zagranie wszystkich trzech akcji z równym prawdopodobieństwem jest równowagą strategii mieszanej.
-
Znajdź wszystkie równowagi następujących gier:
Rysunek 16.20
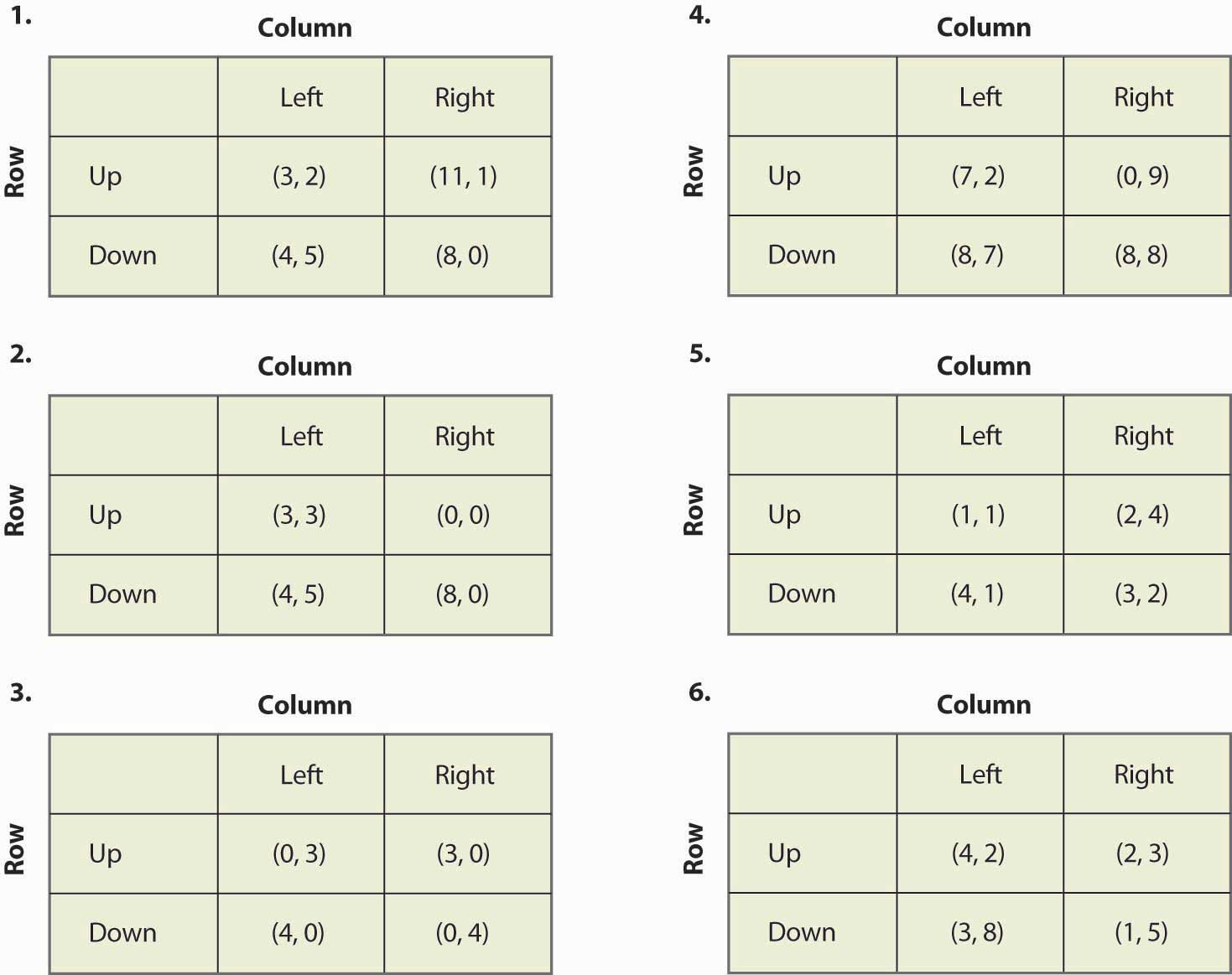
- Jeśli pomnożymy wypłatę gracza przez stałą dodatnią, to równowagi gry nie zmieniają się. Czy to prawda, czy fałsz i dlaczego?