Systemy sterowania – schematy blokowe

Schematy blokowe składają się z pojedynczego bloku lub kombinacji bloków. Służą one do przedstawiania układów sterowania w formie obrazowej.

Podstawowe elementy schematu blokowego

Podstawowymi elementami schematu blokowego są blok, punkt sumowania i punkt startu. Rozważmy schemat blokowy układu sterowania w pętli zamkniętej przedstawiony na poniższym rysunku, aby zidentyfikować te elementy.

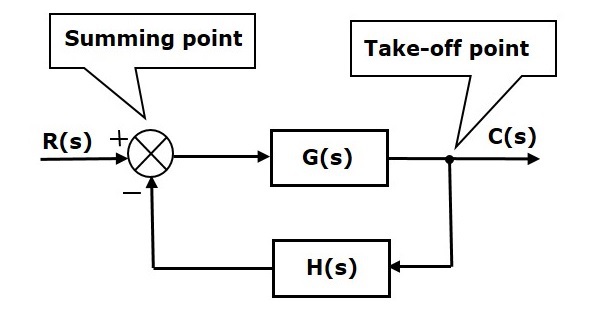
Powyższy schemat blokowy składa się z dwóch bloków posiadających funkcje przenoszenia G(s) i H(s). Posiada on również jeden punkt sumujący i jeden punkt startowy. Strzałki wskazują kierunek przepływu sygnałów. Omówmy teraz te elementy jeden po drugim.

Blok

Funkcja przenoszenia elementu jest reprezentowana przez blok. Blok ma pojedyncze wejście i pojedyncze wyjście.

Następujący rysunek przedstawia blok mający wejście X(s), wyjście Y(s) i funkcję przenoszenia G(s).

Funkcja przeniesienia,$G(s)=frac{Y(s)}{X(s)}$

$$prawa strzałka Y(s)=G(s)X(s)$$

Wyjście bloku uzyskuje się przez pomnożenie funkcji przeniesienia bloku przez wejście.

Punkt sumujący

Punkt sumujący jest reprezentowany przez okrąg z krzyżykiem (X) wewnątrz niego. Ma dwa lub więcej wejść i jedno wyjście. Produkuje algebraiczną sumę wejść. Wykonuje on również sumowanie lub odejmowanie lub kombinację sumowania i odejmowania wejść w oparciu o polaryzację wejść. Zobaczmy te trzy operacje jedna po drugiej.

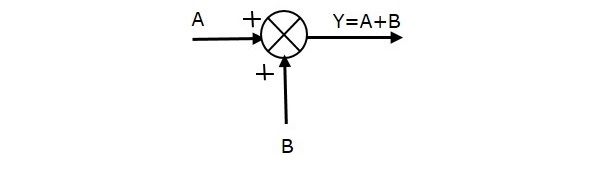
Następny rysunek przedstawia punkt sumowania z dwoma wejściami (A, B) i jednym wyjściem (Y). Tutaj, wejścia A i B mają znak dodatni. Zatem, punkt sumowania wytwarza wyjście, Y jako sumę A i B.

i.e.,Y = A + B.

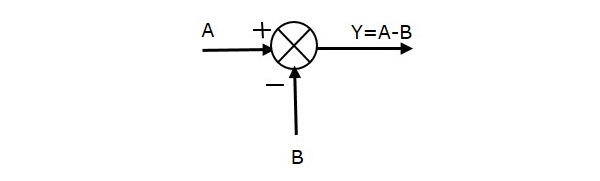
Następny rysunek przedstawia punkt sumowania z dwoma wejściami (A, B) i jednym wyjściem (Y). Tutaj, wejścia A i B mają przeciwne znaki, tzn. A ma znak dodatni, a B ma znak ujemny. Zatem, punkt sumujący wytwarza wyjście Y jako różnicę A i B.

Y = A + (-B) = A – B.

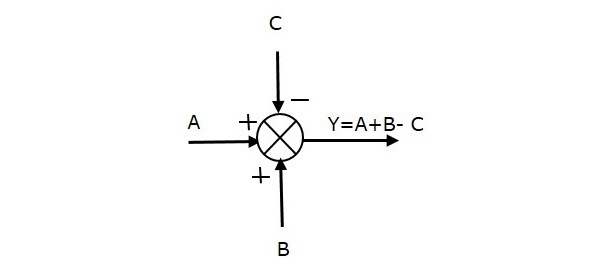
Następny rysunek przedstawia punkt sumujący z trzema wejściami (A, B, C) i jednym wyjściem (Y). Tutaj, wejścia A i B mają znaki dodatnie, a C ma znak ujemny. Tak więc, punkt sumujący produkuje wyjście Y jako

Y = A + B + (-C) = A + B – C.

Punkt odbioru

Punkt odbioru jest punktem, z którego ten sam sygnał wejściowy może być przepuszczony przez więcej niż jedną gałąź. Oznacza to, że za pomocą punktu startowego możemy zastosować to samo wejście do jednego lub więcej bloków, punktów sumujących.

Na poniższym rysunku punkt startowy jest użyty do podłączenia tego samego wejścia, R(s) do dwóch kolejnych bloków.

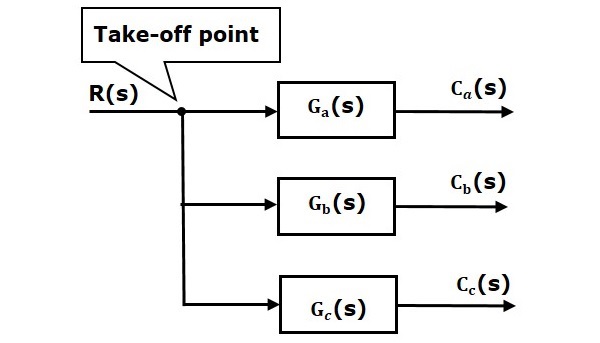
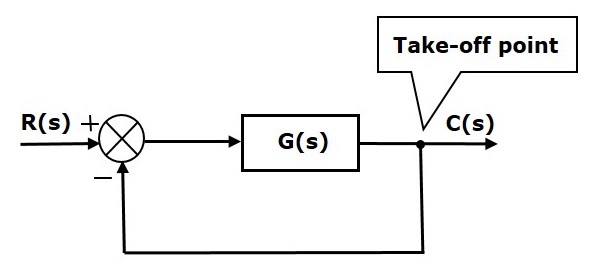
Na poniższym rysunku, punkt startowy służy do podłączenia wyjścia C(s), jako jedno z wejść do punktu sumującego.

Schematy blokowe reprezentacji układów elektrycznych

W tym rozdziale przedstawmy układ elektryczny za pomocą schematu blokowego. Układy elektryczne zawierają głównie trzy podstawowe elementy – rezystor, cewkę i kondensator.

Rozważmy szeregowy obwód RLC, jak pokazano na poniższym rysunku. Gdzie, Vi(t) i Vo(t) są napięciami wejściowymi i wyjściowymi. Niech i(t) będzie prądem przepływającym przez obwód. Ten obwód jest w dziedzinie czasu.

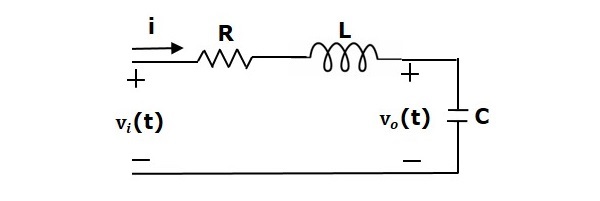
Przez zastosowanie transformaty Laplace’a do tego obwodu, otrzymamy obwód w dziedzinie s. Obwód jest taki, jak pokazano na poniższym rysunku.

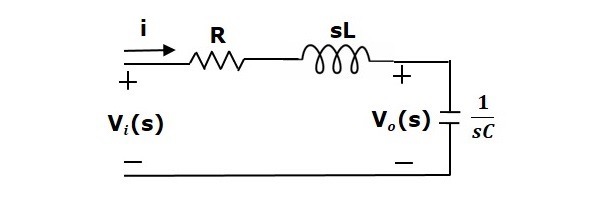
Z powyższego obwodu możemy napisać

$$I(s)=$frac{V_i(s)-V_o(s)}{R+sL}$$

$prawa strzałka I(s)=$lewa \{ \frac{1}{R+sL} \(Równanie 1)

$V_o(s)=left ( \frac{1}{sC} \right )I(s)$ (Równanie 2)

Narysujmy teraz schematy blokowe dla tych dwóch równań osobno. A następnie połączmy odpowiednio te schematy blokowe, aby otrzymać ogólny schemat blokowy szeregu obwodu RLC (s-domena).

Rozwiązanie 1 może być zrealizowane za pomocą bloku posiadającego funkcję przenoszenia, $frac{1}{R+sL}$. Wejście i wyjście tego bloku to $left \{ V_i(s)-V_o(s) \right \}$ i $I(s)$. Potrzebujemy punktu sumowania, aby otrzymać $left \{ V_i(s)-V_o(s) \right \}$. Schemat blokowy równania 1 jest przedstawiony na poniższym rysunku.

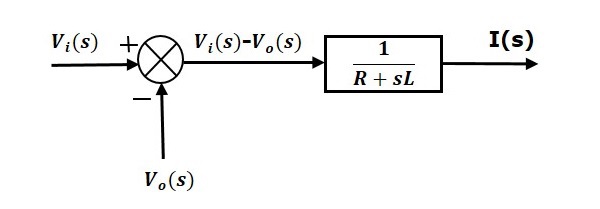
Równanie 2 może być zaimplementowane za pomocą bloku posiadającego funkcję transferu, $frac{1}{sC}$. Wejście i wyjście tego bloku to $I(s)$ i $V_o(s)$. Schemat blokowy równania 2 jest pokazany na poniższym rysunku.

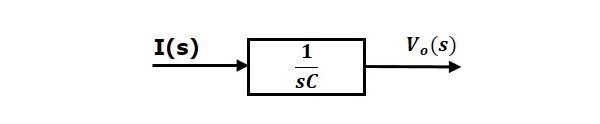
Całościowy schemat blokowy szeregu obwodu RLC (s-domena) jest pokazany na poniższym rysunku.

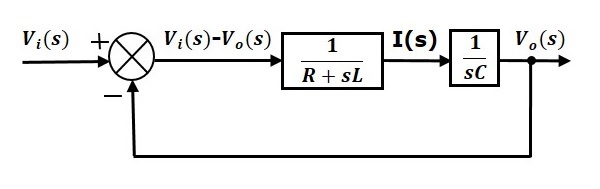
Podobnie, można narysować schemat blokowy dowolnego obwodu elektrycznego lub systemu po prostu postępując zgodnie z tą prostą procedurą.

• Przekształć obwód elektryczny w dziedzinie czasu w obwód elektryczny w dziedzinie s poprzez zastosowanie transformaty Laplace’a.

• Zapisać równania dla prądu przechodzącego przez wszystkie elementy gałęzi szeregowej i napięcia przez wszystkie gałęzie bocznikujące.

• Narysować schematy blokowe dla wszystkich powyższych równań indywidualnie.

• Połącz odpowiednio wszystkie te schematy blokowe, aby otrzymać ogólny schemat blokowy obwodu elektrycznego (s-domena).

.