Talking in Three Dimensions

Przyjrzyjrzyj się temu obrazkowi graniastosłupa prostokątnego:

Ile ma wierzchołków? 8

Ile ma krawędzi? 12

Ile ma twarzy? 6

Łatwe, prawda?

Spróbujmy jeszcze raz. Spójrzmy na ten obrazek stożka:

Ile ma wierzchołków? Czy punkt na szczycie się liczy?

Ile ma krawędzi? Hmm, nie jestem pewien. Czy krawędzie nie powinny być proste?

Ile twarzy? To jest łatwe! Jedna. Na dole jest okrągła ściana. Ale to nie jest wielokąt, więc czy to nadal jest twarz? A jak mam nazwać tę drugą powierzchnię na stożku? Czy ściany nie muszą być płaskie?

Częste pytanie, które otrzymujemy od nauczycieli w klasach 1, 2 i 3 ma związek z tym, jak opisać atrybuty niektórych trójwymiarowych brył, w szczególności cylindrów i stożków. Zgodnie z TEKS, uczniowie powinni opisywać trójwymiarowe bryły używając formalnego języka geometrycznego, takiego jak wierzchołek, krawędź i ściana. Problem polega na tym, że próbujemy używać języka, który działa dla jednej klasy kształtów, aby opisać atrybuty zupełnie innej klasy.

Trójwymiarowe kształty, takie jak graniastosłupy i ostrosłupy są wielościanami. „W geometrii wielościan jest po prostu trójwymiarową bryłą, która składa się ze zbioru wielokątów, zwykle połączonych na krawędziach.” (Źródło) Te bryły mają „płaskie wielokątne twarze, proste krawędzie i wspólne narożniki lub wierzchołki.” (Źródło)

Sfery, cylindry i stożki, z drugiej strony, nie są wielościanami. W rezultacie, nie możemy używać dokładnie tego samego języka do ich opisu, lub jeśli używamy tego samego języka, to ze zrozumieniem, że definicje nie są identyczne. Weźmy na przykład słowo wierzchołek.

Na graniastosłupie prostokątnym, wierzchołek jest ostrym punktem lub rogiem, gdzie spotykają się krawędzie. Graniastosłup prostokątny ma 8 wierzchołków.

Jednakże ten sam termin może być również użyty do opisania punktu stożka. Ten sam termin, ale nie ta sama definicja. Jak mówi Dr Math,

Naprawdę trudna część tutaj jest taka, że „wierzchołek” stożka nie ma nic wspólnego z krawędziami, więc potrzebuje zupełnie nowej definicji; i nie mogę myśleć o naprawdę dobrej definicji na poziomie podstawowym dla tego, co oczywiście mają na myśli, co jest po prostu „punktem.”

Jak studenci będą zajmować się bardziej zaawansowaną matematyką, mogą rozwinąć bardziej wyrafinowany język i definicje. W międzyczasie, gdy są w szkole podstawowej, używamy terminu wierzchołek stożka w RRISD, aby opisać ten atrybut stożka.

Jeśli chcemy, aby uczniowie opisywali i klasyfikowali ten rodzaj trójwymiarowej bryły, to musimy zapewnić przystępny język do tego celu.

Co z innymi atrybutami stożka? Ponownie, naszym celem jest zapewnienie języka, który jest dostępny dla uczniów szkół podstawowych i opisujący te atrybuty, uznając, że nasi uczniowie rozwiną bardziej formalne rozumienie w późniejszym okresie swojej kariery szkolnej. Aby opisać stożek, powiemy, że ma on okrągłą podstawę, czyli płaską powierzchnię, na której spoczywa. Powiemy też, że ma zakrzywioną krawędź wzdłuż podstawy i zakrzywioną powierzchnię, która rozciąga się od tej krawędzi aż do wierzchołka.

A co z walcem? Teraz, gdy mamy już dostępny język do opisu cech stożka, możemy rozszerzyć ten język do opisu cech walca.

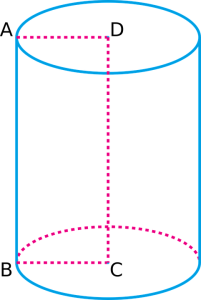
Powyższy walec składa się z dwóch okrągłych podstaw, jednej na górze i jednej na dole. Ma również dwie zakrzywione krawędzie, jedną wzdłuż góry i jedną wzdłuż dołu. Wreszcie ma zakrzywioną powierzchnię, która rozciąga się od dolnej krawędzi aż do górnej krawędzi.

Powinienem dodać, że zarówno stożek jak i walec, które opisałem są stożkiem prostym kołowym i walcem prostym. Podobnie jak w przypadku wielokątów i wielościanów, istnieje wiele innych rodzajów przykładów tych kształtów. Na przykład, stożek lub walec mogą być nachylone, co czyni je skośnymi.

Ważne jest, aby uczniowie widzieli różnorodne przykłady figur dwu- i trójwymiarowych. Im więcej ich spotykają, tym więcej muszą skonfrontować swoich definicji i terminologii, co służy wzmocnieniu ich zrozumienia atrybutów i tego, jak pomagają nam identyfikować i klasyfikować te figury.

Więc jak to wygląda na STAAR?

Na wydanym w 2016 roku teście STAAR zadano pytanie, które dotyczyło właśnie tego tematu i wzmocniło słownictwo, którego używamy w RRISD.

Prawidłowa odpowiedź to F Nie mają wierzchołków. Jeśli spojrzysz na zestaw B, zauważysz, że zawiera on stożek, który, jak mówiliśmy wcześniej, ma wierzchołek. Jeśli Texas Education Agency nie używałaby terminu wierzchołek stożka, to prawdopodobnie widzielibyśmy stożek zawarty w zbiorze A.

Oto myśl przewodnia dr Math:

Jakiej definicji używasz, zależy od tego, co zamierzasz z nią zrobić. Jeśli po prostu opisujesz obiekty, moja luźna definicja jest w porządku. Jeśli masz zamiar udowodnić twierdzenia dotyczące płaszczyzn i kątów, będziesz chciał ograniczyć się do definicji wielokąta, ale wtedy nie będziesz zadawał żadnych pytań o stożki. Myślę, że ludzie często nie zdają sobie sprawy z tego, że nawet jeśli w matematyce zwracamy szczególną uwagę na definicje, to te definicje różnią się w zależności od dziedziny, ponieważ są dostosowane do pewnego kontekstu. To właśnie próbuję zrobić tutaj.

.