Matriisi on numeroiden joukko:

Matriisi
(Tässä on 2 riviä ja 3 saraketta)
Matriisin kertominen yksittäisellä luvulla on helppoa:
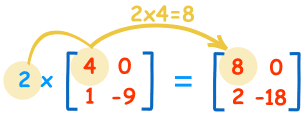
| 2×4=8 | 2×0=0 |
| 2×1=2 | 2×-9=-18 |
Kutsumme lukua (”2” tässä tapauksessa) skalaariarvoksi, joten tätä sanotaan ”skalaarikertoimeksi”.
Matriisin kertominen toisella matriisilla
Mutta kertoaksemme matriisin toisella matriisilla meidän on tehtävä rivien ja sarakkeiden ”pistetuotto” … mitä se tarkoittaa? Katsotaanpa esimerkin avulla:
Tietääksemme vastauksen 1. riville ja 1. sarakkeelle:
”Pistepotenttituote” on se, jossa kerromme toisiaan vastaavat jäsenet ja laskemme sitten yhteen:
(1, 2, 3) – (7, 9, 11) = 1×7 + 2×9 + 3×11
= 58
Sovitamme 1. jäsenet (1 ja 7) yhteen, kerromme ne, samoin 2. jäsenet (2 ja 9) ja 3. jäsenet (3 ja 11), ja lopuksi summaamme ne yhteen.
Haluatko nähdä toisen esimerkin? Tässä se on 1. riville ja 2. sarakkeelle:
(1, 2, 3) – (8, 10, 12) = 1×8 + 2×10 + 3×12
= 64
Voidaan tehdä sama 2. riville ja 1. sarakkeelle:
(4, 5, 6) – (7, 9, 11) = 4×7 + 5×9 + 6×11
= 139
Ja 2. riville ja 2. sarakkeelle:
(4, 5, 6) – (8, 10, 12) = 4×8 + 5×10 + 6×12
= 154
Ja saamme:
VALMIS!
Miksi tehdä näin?
Tämä voi tuntua oudolta ja monimutkaiselta tavalta kertoa, mutta se on välttämätön!
Voin antaa todellisen esimerkin havainnollistamaan, miksi kerromme matriisit tällä tavalla.
Esimerkki: Paikallinen kauppa myy 3 erilaista piirakkaa.
- Omenapiirakat maksavat 3 dollaria kappale
- Kirsikkapiirakat maksavat 4 dollaria kappale
- Mustikkapiirakat maksavat 2 dollaria kappale
Ja tällaisia piirakoita myytiin neljässä päivässä näin paljon:
Ajattele nyt tätä … maanantain myynnin arvo lasketaan näin:
Se on siis itse asiassa hintojen ja myytyjen kappalemäärien ”pistetuotos”:
($3, $4, $2) – (13, 8, 6) = $3×13 + $4×8 + $2×6
= $83
Vastaamme hinnan ja myydyn määrän, kerromme kummatkin ja summaamme tuloksen.
Muuten:
- Myynti maanantaina oli: Omenapiirakat: $3×13=$39, Kirsikkapiirakat: $4×8=$32 ja Mustikkapiirakat: $2×6=$12. Yhdessä se on $39 + $32 + $12 = $83
- Ja tiistaina: $3×9 + $4×7 + $2×4 = $63
- Ja keskiviikkona: $3×7 + $4×4 + $2×0 = $37
- Ja torstaina: $3×15 + $4×6 + $2×3 + $2×4 + $2×4 + $2×4 = $75
On siis tärkeää sovittaa kumpikin hinta kumpaankin määrään.
Nyt tiedät, miksi käytämme ”pistetuotosta”.
Ja tässä on koko tulos matriisimuodossa:

He myivät maanantaina 83 dollarin arvosta piiraita, tiistaina 63 dollarin arvosta jne.
(Voit laittaa nämä arvot matriisilaskuriin nähdäksesi, toimivatko ne.)
Rivit ja sarakkeet
Katsoaksemme, kuinka monta riviä ja saraketta matriisissa on, kirjoitamme usein rivit×sarakkeet.
Esimerkki: Tämä matriisi on 2×3 (2 riviä kertaa 3 saraketta):
Kun teemme kertolaskun:
- Ensimmäisen matriisin sarakkeiden lukumäärän on oltava yhtä suuri kuin toisen matriisin rivien lukumäärän.
- Ja tuloksessa on sama määrä rivejä kuin 1. matriisissa ja sama määrä sarakkeita kuin 2. matriisissa.
Esimerkki:

Tässä esimerkissä kerroimme 1×3-matriisin 3×4-matriisilla (huomaa, että 3:t ovat samat), ja tuloksena oli 1×4-matriisi.
Yleisesti:
Kerrottaaksemme m×n-matriisin n×p-matriisilla, ns:n on oltava samat,
ja tuloksena on m×p-matriisi.
![]()
Selvä … kertomalla 1×3 3×1:llä saadaan 1×1 tulos:
Mutta kertomalla 3×1:n 1×3:lla saadaan tulos 3×3:
Identiteettimatriisi
Identiteettimatriisi on numeroa ”1” vastaava matriisi:
A 3×3 Identiteettimatriisi
- Se on ”neliömäinen” (siinä on sama määrä rivejä kuin sarakkeita)
- Se voi olla suuri tai pieni (2×2, 100×100, … mitä tahansa)
- Sen päädiagonaalilla on 1:t ja kaikkialla muualla 0:t
- Sen symboli on isolla I-kirjaimella
Se on erityinen matriisi, koska kun kerromme sillä, alkuperäinen ei muutu:
A × I = A
I × A = A
Kertomisen järjestys
Aritmetiikassa olemme tottuneet:
3 × 5 = 5 × 3
(Kertolaskun kommutatiivinen laki)
Mutta tämä ei yleensä päde matriiseille (matriisien kertolasku ei ole kommutatiivinen):
AB ≠ BA
Kun muutamme kertolaskun järjestystä, vastaus on (yleensä) erilainen.
Esimerkki:
Katso, miten järjestyksen muuttaminen vaikuttaa tähän kertolaskuun:
Se voi johtaa samaan tulokseen (esimerkiksi kun yksi matriisi on identiteettimatriisi), mutta ei yleensä.




