A mátrix számok tömbje:

A mátrix
(Ennek 2 sora és 3 oszlopa van)
A mátrix szorzása egyetlen számmal egyszerű:
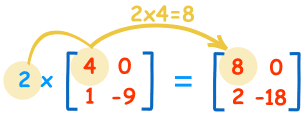
| 2×4=8 | 2×0=0 |
| 2×1=2 | 2×-9=-18 |
A számot (“2” ebben az esetben) skalárnak nevezzük, ezért ezt “skaláris szorzásnak” hívjuk.
Mátrix szorzása egy másik mátrixszal
De ahhoz, hogy egy mátrixot megszorozzunk egy másik mátrixszal, a sorok és oszlopok “pontszorzatát” kell elvégeznünk … ez mit jelent? Nézzük meg egy példával:
Az 1. sor és az 1. oszlop válaszának kiszámításához:
A “ponttétel” az, amikor az egyező tagokat szorozzuk, majd összegezzük:
(1, 2, 3) – (7, 9, 11) = 1×7 + 2×9 + 3×11
= 58
Az 1. tagokat (1 és 7) összevetjük, megszorozzuk őket, ugyanígy a 2. tagokat (2 és 9) és a 3. tagokat (3 és 11), végül összegezzük őket.
Akarsz látni egy másik példát? Itt van az 1. sorra és a 2. oszlopra:
(1, 2, 3) – (8, 10, 12) = 1×8 + 2×10 + 3×12
= 64
Megtehetjük ugyanezt a 2. sor és az 1. oszlop esetében is:
(4, 5, 6) – (7, 9, 11) = 4×7 + 5×9 + 6×11
= 139
És a 2. sor és a 2. oszlop esetében is:
(4, 5, 6) – (8, 10, 12) = 4×8 + 5×10 + 6×12
= 154
És megkapjuk:
KÉSZ!
Miért csináljuk így?
A szorzásnak ez a módja furcsának és bonyolultnak tűnhet, de szükség van rá!
Mutathatok egy valós példát arra, hogy miért így szorozzuk a mátrixokat.
Példa: A helyi boltban 3 féle pitét árulnak.
- Az almás pite darabja 3 dollárba kerül
- A meggyes pite darabja 4 dollárba
- Az áfonyás pite darabja 2 dollárba kerül
És ennyit adtak el 4 nap alatt:
Most gondolkodj el ezen … a hétfői eladások értékét így számoljuk ki:
Ez tehát valójában az árak és az eladott mennyiségek “pontterméke”:
($3, $4, $2) – (13, 8, 6) = $3×13 + $4×8 + $2×6
= $83
Egyeztetjük az árat azzal, hogy mennyi fogyott, megszorozzuk mindkettőt, majd az eredményt összegezzük.
Más szavakkal:
- A hétfői eladások a következők voltak: Almás piték: 3×13=39 dollár, cseresznyés piték: 4×8=32 dollár, áfonyás piték: 2×6=12 dollár. Ez együtt 39$ + 32$ + 12$ = 83$
- És kedden: 3$×9$ + 4$×7$ + 2$×4$ = 63$
- És szerdán: 3$×7$ + 4$×4$ + 2$×0$ = 37$
- És csütörtökön: 3$×15$ + 4$×6$ + 2$×3$ = 75$
Ezért fontos, hogy minden árat minden mennyiséghez igazítsunk.
Most már tudod, hogy miért használjuk a “pont szorzatot”.
És itt a teljes eredmény mátrix formában:

Hétfőn 83 dollár értékben adtak el pitét, kedden 63 dollárt, stb.
(Ezeket az értékeket beírhatod a Mátrixkalkulátorba, hogy megnézd, működnek-e.)
Sorok és oszlopok
Hogy megmutassuk, hány sora és oszlopa van egy mátrixnak, gyakran azt írjuk, hogy sorok×oszlopok.
Példa: Ez a mátrix 2×3 (2 sor x 3 oszlop):
Ha szorzást végzünk:
- Az 1. mátrix oszlopainak száma egyenlő kell legyen a 2. mátrix sorainak számával.
- Az eredménynek pedig ugyanannyi sora lesz, mint az 1. mátrixnak, és ugyanannyi oszlopa, mint a 2. mátrixnak.
Példa:

Ebben a példában egy 1×3-as mátrixot szoroztunk meg egy 3×4-es mátrixszal (figyeljük meg, hogy a 3-asok azonosak), és az eredmény egy 1×4-es mátrix lett.
Általános:
Hogy egy m×n mátrixot megszorozzunk egy n×p mátrixszal, az ns-nek azonosnak kell lennie,
és az eredmény egy m×p mátrix lett.
![]()
Szóval … egy 1×3 szorozva egy 3×1-gyel 1×1-es eredményt kapunk:
De a 3×1 szorzása 1×3-mal 3×3 eredményt ad:
Identitásmátrix
Az “Identitásmátrix” az “1” szám mátrix-egyenértéke:
A 3×3-as azonossági mátrix
- Ez “négyzet” (ugyanannyi sora van, mint ahány oszlopa)
- Ez lehet nagy vagy kicsi (2×2, 100×100, … akármilyen)
- A főátlóján 1-es, mindenhol máshol 0-s
- Szimbóluma az I nagybetű
Ez egy speciális mátrix, mert ha szorzunk vele, az eredeti változatlan marad:
A × I = A
I × A = A
A szorzás rendje
A számtanban megszoktuk:
3 × 5 = 5 × 3
(A szorzás kommutatív törvénye)
De ez általában nem igaz a mátrixokra (a mátrixszorzás nem kommutatív):
AB ≠ BA
Ha megváltoztatjuk a szorzás sorrendjét, a válasz (általában) más lesz.
Példa:
Nézzük meg, hogy a sorrend megváltoztatása hogyan befolyásolja ezt a szorzást:
A válaszok eltérőek!
Ez lehet azonos eredmény (például ha az egyik mátrix az azonossági mátrix), de általában nem.




