行列は数字の配列です:

行列
(これは2行3列です)
行列に一つの数字を掛けるのは簡単です:
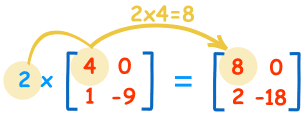
| 2×4=8 | 2×0=0 |
| 2×1=2 | 2×9=-18 |
数(ここでは「2」)はスカラということから「スカラー掛け」と言いますが、これは「2×0」です。
行列と別の行列の掛け算
しかし、行列と別の行列を掛け合わせるには、行と列の「内積」を行う必要があります・・・これはどういうことでしょうか? 例で見てみましょう。
1行と1列の答えを出すには:
「ドットプロダクト」とは、一致するメンバーを掛け合わせて、合計を出すことです。
(1, 2, 3) – (7, 9, 11) = 1×7 + 2×9 + 3×11
= 58
第1メンバー(1、7)をマッチさせて掛け、第2メンバー(2、9)、第3メンバー(3、11)も同様に掛けて、最後にそれらを足し算をします。
別の例を見てみましょうか。 これは1行目と2列目についてです。
(1, 2, 3) – (8, 10, 12) = 1×8 + 2×10 + 3×12
= 64
同じことを、2行目と1列目についても行うことができます。
(4, 5, 6) – (7, 9, 11) = 4×7 + 5×9 + 6×11
= 139
そして2行目と2列目についても同じようにします。
(4, 5, 6) – (8, 10, 12) = 4×8 + 5×10 + 6×12
= 154
そして、次のようになります:
DONE!
DONE!
Why Do It This Way?
これは奇妙で複雑な乗算の方法に見えるかもしれませんが、必要なのです!
なぜこの方法で行列を乗せるのかを説明するために実例をあげましょう。
- Apple pies cost $3 each
- Cherry pies cost $4 each
- Blueberry pies cost $2 each
And this is how many they sold in 4 days:
Now think about this …. 月曜日の販売額は次のように計算されます:
つまり、実際には価格と販売数の「点積」なんですね。
($3, $4, $2) – (13, 8, 6) = $3×13 + $4×8 + $2×6
= $83
価格と販売数を合わせ、それぞれをかけて、その結果を合計するのです。
つまり、
- 月曜日の売上は、以下の通り。 アップルパイ:3×13=$39、チェリーパイ:4×8=$32、ブルーベリーパイ:2×6=$12でした。 合わせて39ドル+32ドル+12ドル=83ドル
- そして火曜日は:3×9ドル+4×7ドル+2×4ドル=63ドル
- そして水曜日は:3×7ドル+4×4ドル+2×0ドル=37ドル
- そして木曜日は:3×15ドル+4×6ドル+2×3ドル=75ドル
だから各数値と各数を一致させることが重要なのです。
これで「ドット積」を使う理由がわかりましたね。
そして、これがマトリックス形式の完全な結果です:

彼らは月曜日に83ドル分のパイを売り、火曜日に63ドル分を売った、などです。
(これらの値を行列計算機に入れて、うまくいくかどうか確認できます。)
行と列
行列が何行と列を持っているかを示すには、行×列をよく書きます。
の例です。 この行列は2×3(2行×3列)です。
乗算するとき:
- 第1の行列の列数は第2の行列の行数と同じでなければなりません。
例:

その例では、1×3行列に3×4行列(3が同じであることに注意)を掛け、その結果は1×4行列でした。
一般的には、1×4行列です。
m×n行列とn×p行列を掛けるには、nsが同じでなければならず、
その結果はm×p行列となります。
![]()
そこで … 1×3に3×1を掛けると1×1になります。
ただし3×1に1×3をかけると3×3の結果になる。
Identity Matrix
「ID行列」は、数字「1」に相当する行列である。
3×3の恒等式行列
- それは「正方」(列と行の数が同じ)
- それは大きくても小さくてもよい(2×2、100×100、……)。..
- 主対角線上に1があり、それ以外は0である
- 記号は大文字のI
乗算しても元の行列は変化しないので、特殊な行列であると言える。
A × I = A
I × A = A
乗算の順序
算数で私たちは慣れています。
3 × 5 = 5 × 3
(乗法の可換法)
しかし、これは行列の場合は一般に正しくありません(行列の乗法は可換ではない):
AB ≠ BA
乗法の順番を変えると答えは(通常)違ってくるのです。
の例です。
順番を変えると、この掛け算にどう影響するかを見てみましょう。
=
答えはバラバラ!
同じ結果になることもありますが(1つの行列が恒等式行列の場合など)、通常はありません。




