Een Matrix is een matrix van getallen:

Een Matrix
(Deze heeft 2 Rijen en 3 Kolommen)
Een matrix met één getal vermenigvuldigen is eenvoudig:
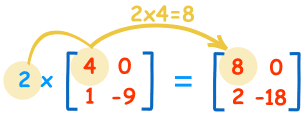
| 2×4=8 | 2×0=0 |
| 2×1=2 | 2×-9=-18 |
Het getal (“2” in dit geval) noemen we een scalair, dus dit heet “scalaire vermenigvuldiging”.
Vermenigvuldiging van een matrix met een andere matrix
Maar om een matrix met een andere matrix te vermenigvuldigen moeten we het “dot-product” van rijen en kolommen doen … wat betekent dat? Laten we eens kijken met een voorbeeld:
Om het antwoord voor de 1e rij en 1e kolom uit te rekenen:
Het “dot-product” is waar we overeenkomende leden vermenigvuldigen, en dan optellen:
(1, 2, 3) – (7, 9, 11) = 1×7 + 2×9 + 3×11
= 58
We vermenigvuldigen de 1e leden (1 en 7), vermenigvuldigen ze, evenzo voor de 2e leden (2 en 9) en de 3e leden (3 en 11), en tellen ze tenslotte bij elkaar op.
Wilt u nog een voorbeeld zien? Hier is het voor de 1e rij en 2e kolom:
(1, 2, 3) – (8, 10, 12) = 1×8 + 2×10 + 3×12
= 64
Hetzelfde kunnen we doen voor de 2e rij en 1e kolom:
(4, 5, 6) – (7, 9, 11) = 4×7 + 5×9 + 6×11
= 139
En voor de 2e rij en 2e kolom:
(4, 5, 6) – (8, 10, 12) = 4×8 + 5×10 + 6×12
= 154
En we krijgen:
DONE!
Waarom doen we het op deze manier?
Dit lijkt misschien een vreemde en ingewikkelde manier van vermenigvuldigen, maar het is nodig!
Ik kan u een voorbeeld uit de praktijk geven om te illustreren waarom we matrices op deze manier vermenigvuldigen.
Voorbeeld: De plaatselijke winkel verkoopt 3 soorten taarten.
- Apple taarten kosten $3 per stuk
- Cherry taarten kosten $4 per stuk
- Blueberry taarten kosten $2 per stuk
En dit is hoeveel ze er in 4 dagen verkocht hebben:
Nou denk hier eens over na … de waarde van de verkoop voor maandag wordt zo berekend:
Dus het is in feite het “dot-product” van de prijzen en het aantal verkochte exemplaren:
($3, $4, $2) – (13, 8, 6) = $3×13 + $4×8 + $2×6
= $83
We vergelijken de prijs met het aantal verkochte exemplaren, vermenigvuldigen elk, en tellen dan het resultaat op.
In andere woorden:
- De verkopen voor maandag waren: Appeltaarten: $3×13=$39, Kersentaarten: $4×8=$32, en Bosbessentaarten: $2×6=$12. Samen is dat $39 + $32 + $12 = $83
- En voor dinsdag: $3×9 + $4×7 + $2×4 = $63
- En voor woensdag: $3×7 + $4×4 + $2×0 = $37
- En voor donderdag: $3×15 + $4×6 + $2×3 = $75
Het is dus van belang om elke prijs af te stemmen op elke hoeveelheid.
Nu weet je waarom we het “punt product” gebruiken.
En hier is het volledige resultaat in matrixvorm:

Ze hebben op maandag voor 83 dollar aan taarten verkocht, op dinsdag voor 63 dollar, enzovoort.
(U kunt deze waarden in de Matrix Calculator stoppen om te zien of ze werken.)
Rijen en kolommen
Om aan te geven hoeveel rijen en kolommen een matrix heeft, schrijven we vaak rijen×kolommen.
Voorbeeld: Deze matrix is 2×3 (2 rijen bij 3 kolommen):
Wanneer we vermenigvuldigen:
- Het aantal kolommen van de 1e matrix moet gelijk zijn aan het aantal rijen van de 2e matrix.
- En het resultaat zal hetzelfde aantal rijen hebben als de 1e matrix, en hetzelfde aantal kolommen als de 2e matrix.
Voorbeeld:

In dat voorbeeld vermenigvuldigden we een 1×3 matrix met een 3×4 matrix (merk op dat de 3-en hetzelfde zijn), en het resultaat was een 1×4 matrix.
In het algemeen:
Om een m×n matrix met een n×p matrix te vermenigvuldigen, moeten de ns gelijk zijn,
en het resultaat is een m×p matrix.
Dus … als je een 1×3 met een 3×1 vermenigvuldigt, krijg je een 1×1 als resultaat:
Maar als je een 3×1 met een 1×3 vermenigvuldigt, krijg je een 3×3 als uitkomst:
Identiteitsmatrix
De “Identiteitsmatrix” is het matrixequivalent van het getal “1”:
Een 3×3 Identiteitsmatrix
- Hij is “vierkant” (heeft evenveel rijen als kolommen)
- Hij kan groot of klein zijn (2×2, 100×100, … wat dan ook)
- Het heeft 1-en op de hoofddiagonaal en 0-en overal elders
- Het symbool is de hoofdletter I
Het is een speciale matrix, want als we er mee vermenigvuldigen, blijft het origineel ongewijzigd:
A × I = A
I × A = A
Orde van vermenigvuldiging
In de rekenkunde zijn we gewend aan:
3 × 5 = 5 × 3
(De commutatieve wet van vermenigvuldiging)
Maar dit geldt in het algemeen niet voor matrices (matrixvermenigvuldiging is niet commutatief):
AB ≠ BA
Wanneer we de volgorde van vermenigvuldiging veranderen, is het antwoord (meestal) anders.
Voorbeeld:
Zie hoe het veranderen van de volgorde deze vermenigvuldiging beïnvloedt:
De antwoorden zijn verschillend!
Het kan tot hetzelfde resultaat leiden (zoals wanneer één matrix de Identiteitsmatrix is) maar meestal niet.




