Arkimediske spiraler bruges ofte i analysen af induktionsspoler, spiralvarmevekslere og mikrofluidiske enheder. I dag vil vi demonstrere, hvordan man opbygger en arkimedisk spiral ved hjælp af analytiske ligninger og deres derivater til at definere et sæt spiralkurver. Baseret på disse kurver vil vi derefter skabe en 2D-geometri med en specifik tykkelse og ekstrudere den til en fuld 3D-geometri.
En kort introduktion til arkimediske spiraler
Spiraler, eller spiraler, eller spiraler, der er almindeligt observeret i naturen, anvendes i mange tekniske konstruktioner. Som elektroingeniør kan man f.eks. vikle induktionsspoler i spiralformede mønstre og konstruere spiralformede antenner. Som maskiningeniør kan du bruge spiraler ved udformning af fjedre, spiralformede tandhjul eller endog den urmekanisme, der er fremhævet nedenfor.

Eksempel på en arkimedisk spiral, der anvendes i en urmekanisme. Billede af Greubel Forsey. Licensed by CC BY-SA 3.0, via Wikimedia Commons.
Her vil vi fokusere på en bestemt type spiral, nemlig den, der indgår i den mekanisme, der er vist ovenfor: en arkimedisk spiral. En arkimedisk spiral er en type spiral, der har en fast afstand mellem sine på hinanden følgende vindinger. Denne egenskab gør det muligt at anvende den i vid udstrækning til konstruktion af flade spiraler og fjedre.
Vi kan beskrive en arkimedisk spiral med følgende ligning i polære koordinater:
hvor a og b er parametre, der definerer spiralens begyndelsesradius og afstanden mellem dens på hinanden følgende vindinger, hvoraf sidstnævnte er lig med 2 \pi b. Bemærk, at en arkimedisk spiral undertiden også kaldes en aritmetisk spiral. Dette navn stammer fra den aritmetiske progression af afstanden fra oprindelsen til punktet på den samme radial.
Design af en parametriseret arkimedisk spiralgeometri
Nu da vi har introduceret arkimediske spiraler, skal vi se på, hvordan man parameteriserer og skaber et sådant design til analyse i COMSOL Multiphysics.
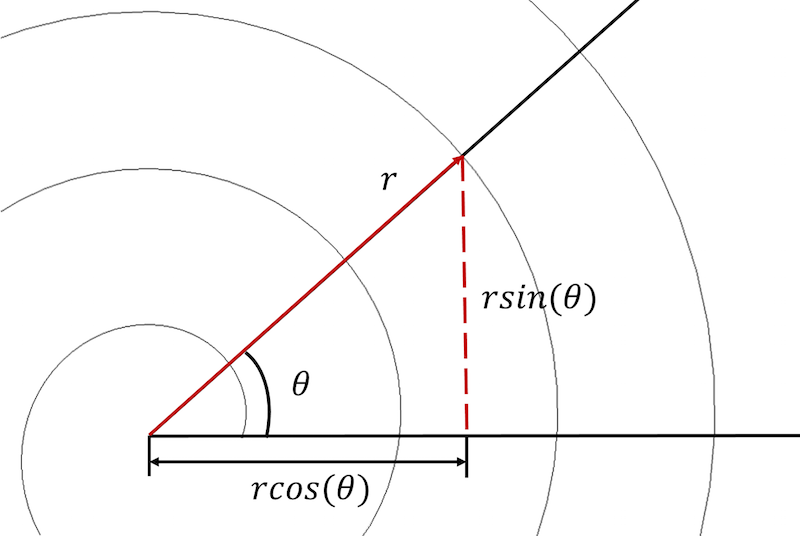
En arkimedisk spiral kan beskrives i både polære og kartesiske koordinater.
For at begynde skal vi konvertere spiralens ligninger fra et polært til et kartesisk koordinatsystem og udtrykke hver ligning i en parametrisk form:
x_{komponent}=rcos(\theta) \\
y_{komponent}=rsin(\theta)
\end{align*}
Denne transformation giver os mulighed for at omskrive den arkimediske spirals ligning i en parametrisk form i det kartesiske koordinatsystem:
x_{komponent}=(a+b\theta)cos(\theta) \\
y_{komponent}=(a+b\theta)sin(\theta)
\end{align*}
I COMSOL Multiphysics er det nødvendigt at træffe beslutning om det sæt parametre, der skal definere spiralens geometri. Disse parametre er spiralens begyndelsesradius a_{initial}, spiralens slutradius a_{final} og det ønskede antal omgange n. Spiralens væksthastighed b kan derefter udtrykkes som:
Det er endvidere nødvendigt at træffe beslutning om spiralens startvinkel theta_0 og slutvinkel theta_f. Lad os begynde med værdierne theta_0=0 og theta_f=2 \pi n. Med disse oplysninger er vi i stand til at definere et sæt parametre for spiralgeometrien.
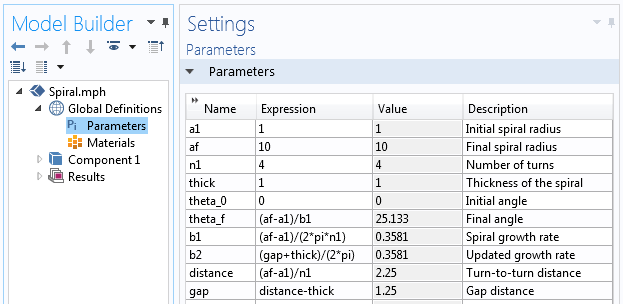
De parametre, der bruges til at opbygge spiralgeometrien.
For at opbygge denne spiral starter vi med en 3D-komponent og opretter et arbejdsplan i Geometri-grenen. I arbejdsplanets geometri tilføjer vi derefter en parametrisk kurve og bruger de parametriske ligninger, der er refereret ovenfor, med en varierende vinkel til at tegne en 2D-version af den arkimediske spiral. Disse ligninger kan indtastes direkte i den parametriske kurves Udtryksfelt, eller vi kan først definere hver ligning i en ny Analytisk funktion som:
X_{fun}=(a+bs)cos(s) \\
Y_{fun}=(a+bs)sin(s) \\
\end{align*}
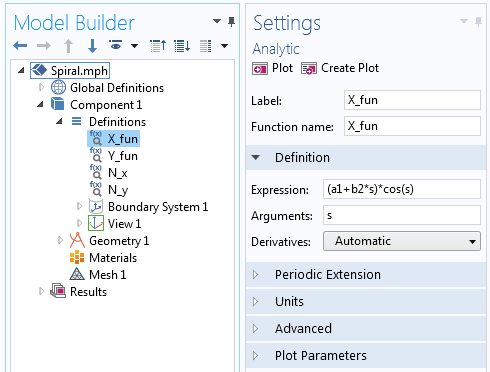
X-komponenten af ligningen for den arkimediske spiral, der er defineret i den analytiske funktion.
Den analytiske funktion kan anvendes i udtrykkene for den parametriske kurve. I denne Parametriske kurve varierer vi parameter s fra spiralens begyndelsesvinkel, theta_0, til spiralens slutvinkel, theta_f=2 \pi n.
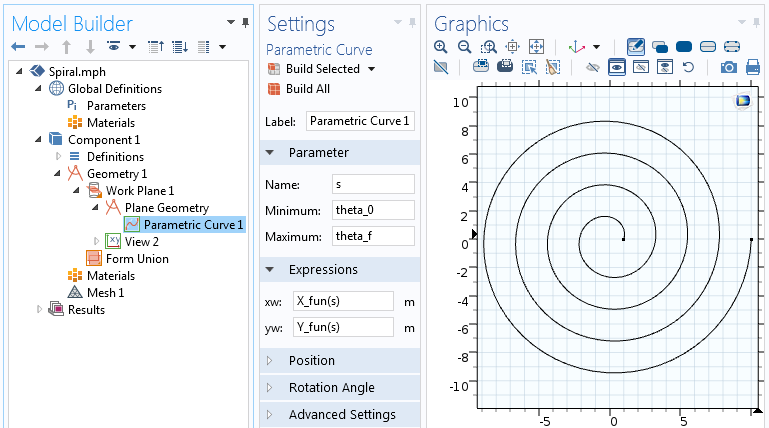
Indstillingerne for funktionen Parametrisk kurve.
De parametriske spiralligninger, der anvendes i funktionen Parametrisk kurve, vil resultere i en spiral repræsenteret ved en kurve. Lad os nu bygge videre på denne geometri og tilføje tykkelse til den for at skabe et 2D-solidobjekt.
Hertil er vores spiral blevet parameteriseret med hensyn til den indledende radius a_{initial}, den endelige radius a_{final} og det ønskede antal omgange n. Nu skal vi indarbejde tykkelsen som endnu en kontrolparameter i spiralens ligning.
Lad os begynde med spiralens vigtigste egenskab, som siger, at afstanden mellem spiralens vindinger er lig med 2 \pi b. Dette svarer også til \frac{a_{final}-a_{initial}}}{n}. For at indarbejde tykkelsen repræsenterer vi afstanden mellem hver enkelt spiralomgang som en sum af spiralens tykkelse og det resterende mellemrum mellem omgange, thick+gap.
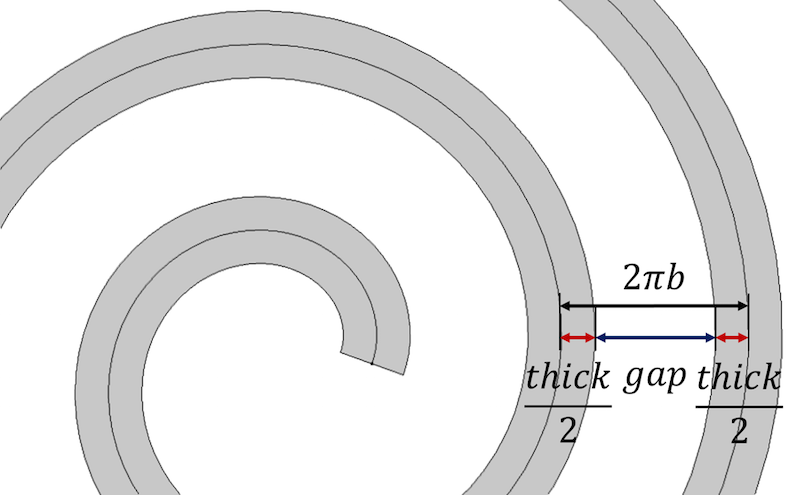
Afstanden mellem spiralens omgange er defineret ud fra spiralens tykkelse og mellemrumsparametre.
For at kontrollere tykkelsen og opnå identisk afstand mellem spiralerne kan afstanden udtrykkes som:
distance=\frac{a_{initial}-a_{final}}}{n} \\\
gap=distance-thick
\end{align*}
Efter at have defineret tykkelse og udtrykt mellemrummet mellem vindinger i form af tykkelse og konstant afstand mellem spiralens centerlinjer, kan vi omskrive spiralvækstparameteren i form af tykkelse som:
distance=2\pi b \\
b=\frac{gap+tykkelse}{2\pi}
\end{align*}
Vi ønsker også at udtrykke spiralens endelige vinkel i form af dens indledende og endelige radier:
\theta_{final}=2 \pi n \\
a_{final}=\text{samlet afstand}+a_{initial} \\
a_{final}=2 \pi bn+a_{initial} \\
n=\frac{a_{final}-a_{initial}}}{2 \pi b} \\
\theta_{final}=\frac{2 \pi (a_{{final}-a_{initial})}{2 \pi b} \\
\theta_{final}=\frac{a_{final}-a_{initial}}}{b}
\end{align*}
Vil du starte spiralen fra en anden vinkel end nul? I så fald skal du tilføje denne begyndelsesvinkel til din slutvinkel i udtrykket for parameteren: theta_f=\frac{a_{{final}-a_{initial}}}{b}+theta_0.
Duplikerer man den eksisterende spiralkurve to gange og placerer disse kurver med en forskydning på -\frac{thick}{2} og +\frac{thick}{2} i forhold til den oprindelige spiralkurve, kan man opbygge spiralen med tykkelse. For at placere den øverste og nederste spiral korrekt skal vi sikre os, at de forskudte spiraler er normale i forhold til den oprindelige spiralkurve. Dette kan opnås ved at multiplicere forskydningsafstanden \pm\frac{thick}{2} med enhedsvektoren, der er normal til spiralkurven. Ligningerne for de normale vektorer til en kurve i parametrisk form er:
hvor s er den parameter, der anvendes i den parametriske kurvefunktion. For at få en enhedsnormal skal vi dividere disse udtryk med længden af normalen:
Vores opdaterede parametriske ligninger for den arkimediske spiral med et halvt tykkelsesforskydning er:
x_{component}=(a+bs)cos(s)-\frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}\frac{thick}{2} \\\
y_{komponent}=(a+bs)sin(s)+\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}}\frac{thick}{2}
\end{align*}
At skrive disse ligninger i den parametriske kurves udtryksfelter kan være ret tidskrævende. Som sådan introducerer vi følgende notation:
N_x=-\frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}} \\
N_y=\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2 }}
\end{align*}
hvor hver N_x og N_y er defineret via den analytiske funktion i COMSOL Multiphysics, på samme måde som vi definerede X_{fun} og Y_{fun} for den første parametriske kurve. I funktionen bruger vi differentieringsoperatoren d(f(x),x) til at tage den afledte værdi, som vist på følgende skærmbillede.
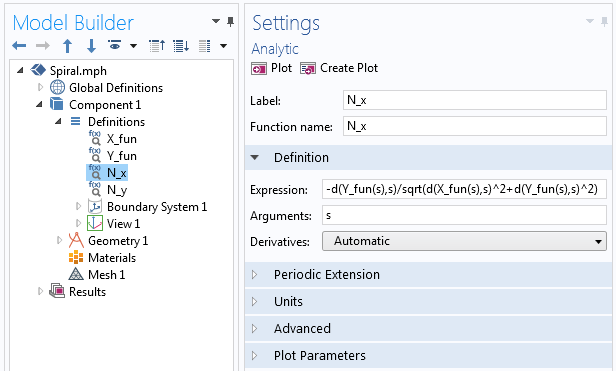
Eksempler på den afledte operatør, der anvendes i den analytiske funktion.
Funktionerne X_{fun}, Y_{fun}, N_x og N_y kan derefter bruges direkte i den parametriske kurves udtryk for kurven på den ene side:
x_{lower}=X_{fun}(s)+N_x(s)\frac{thick}{2} \\
y_{lower}=Y_{fun}(s)+N_y(s)\frac{thick}{2}
\end{align*}
Funktionerne kan også bruges til kurven på den anden side:
x_{opper}=X_{fun}(s)-N_x(s)\frac{thick}{2} \\
y_{upper}=Y_{fun}(s)-N_y(s)\frac{thick}{2}
\end{align*}
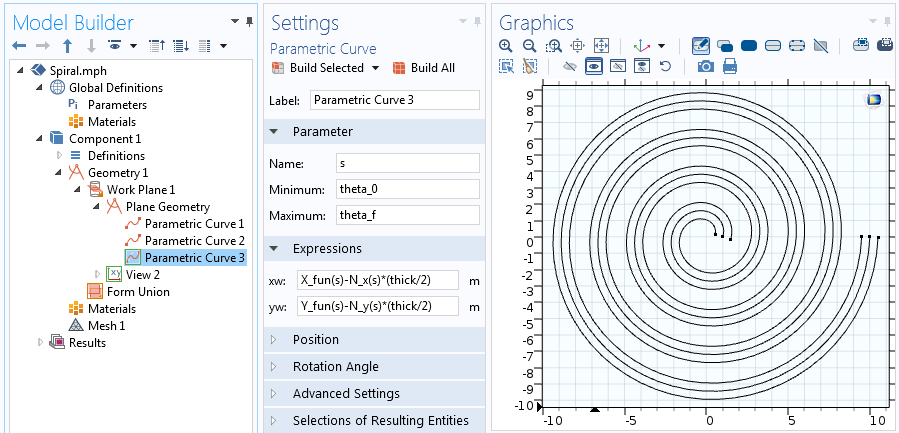
Sammenligninger for den anden af de to forskudte parametriske kurver.
For at forbinde enderne af to kurver tilføjer vi yderligere to parametriske kurver ved hjælp af en lille modifikation af de ovennævnte ligninger. For den kurve, der slutter sig til spiralens centrum, skal vi evaluere X_{fun}, Y_{fun}, N_x og N_y for startværdien af vinklen, theta. For den kurve, der slutter sig til spiralens yderside, skal vi vurdere den endelige værdi af theta. Derfor er den sammenføjende kurve i midten:
X_{fun}(theta_0)+s\cdot N_x(theta_0)\cdot\frac{thick}{2} \\
Y_{fun}(theta_0)+s\cdot N_y(theta_0)\cdot\frac{thick}{2}
\end{align*}
Den ydre sammenføjningskurve er i mellemtiden:
X_{fun}(theta_f)+s\cdot N_x(theta_f)\cdot\frac{thick}{2} \\
Y_{fun}(theta_f)+s\cdot N_y(theta_f)\cdot\frac{thick}{2}
\end{align*}
I begge ovenstående ligninger går s fra -1 til +1, som vist i skærmbilledet nedenfor.
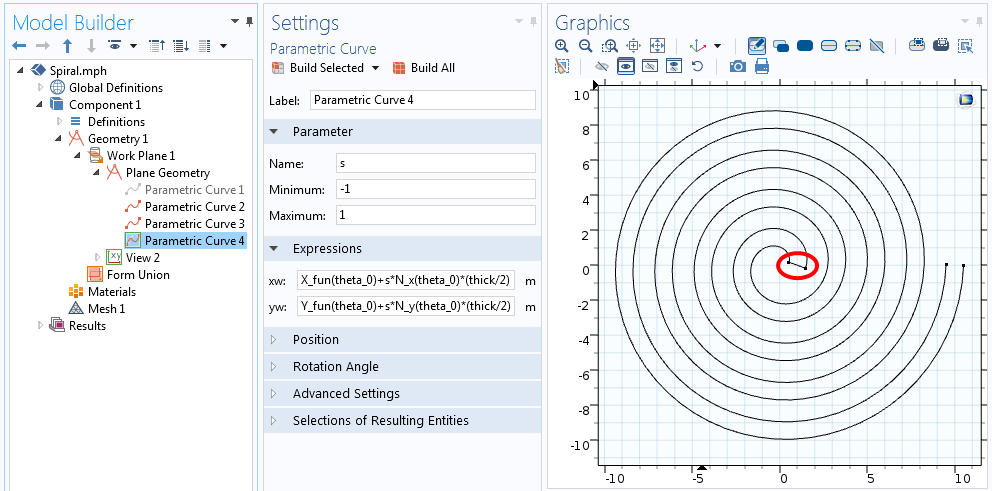
Ligninger for den kurve, der slutter sig til den ene ende af spiralen.
Vi har nu fem kurver, der definerer spiralens midterlinje og alle fire sider af profilen. Vi kan deaktivere (eller endda slette) den kurve, der beskriver centerlinjen, da den ikke er virkelig nødvendig, så vi kun har spiralens omrids tilbage. Med omridset af vores spiral defineret kan operationen Konverter til Solid bruges til at oprette et enkelt geometriobjekt. Denne 2D-spiral kan endelig ekstruderes til 3D via Extrude-operationen.
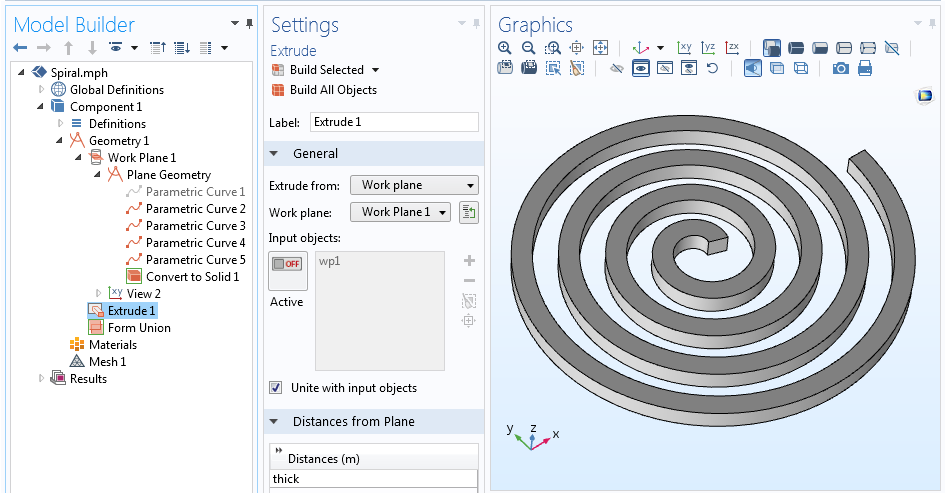
Den fulde geometriske sekvens og den ekstruderede 3D-spiralgeometri.
Sluttende bemærkninger om modellering af arkimediske spiraler i COMSOL Multiphysics
Vi har gennemgået trinene til oprettelse af en fuldt parametriseret arkimedisk spiral. Med denne spiralgeometri kan du ændre enhver af parametrene og eksperimentere med forskellige designs eller endda bruge dem som parametre i en optimeringsundersøgelse. Vi opfordrer dig til at bruge denne teknik i dine egne modelleringsprocesser, så du kan fremme analysen af dit særlige spiralbaserede tekniske design.