Arkimedisk spiral används ofta i analysen av induktorslingor, spiralvärmeväxlare och mikrofluidiska enheter. Idag ska vi visa hur man bygger en arkimedisk spiral med hjälp av analytiska ekvationer och deras derivat för att definiera en uppsättning spiralkurvor. Baserat på dessa kurvor kommer vi sedan att skapa en 2D-geometri med specifik tjocklek och extrudera den till en fullständig 3D-geometri.
En kort introduktion till arkimediska spiraler
Spiraler eller spiraler, eller spiraler, som är allmänt observerade i naturen, används i många tekniska konstruktioner. Som elektrotekniker kan man till exempel linda induktiva spolar i spiralmönster och konstruera spiralformade antenner. Som maskiningenjör kan du använda spiraler när du utformar fjädrar, spiralformade kugghjul eller till och med den klockmekanism som visas nedan.

Ett exempel på en arkimedisk spiral som används i en klockmekanism. Bild av Greubel Forsey. Licensed by CC BY-SA 3.0, via Wikimedia Commons.
Här kommer vi att fokusera på en specifik typ av spiral, den som används i mekanismen som visas ovan: en arkimedisk spiral. En arkimedisk spiral är en typ av spiral som har ett fast avstånd mellan sina på varandra följande varv. Denna egenskap gör att den kan användas i stor utsträckning vid konstruktion av platta spiraler och fjädrar.
Vi kan beskriva en arkimedisk spiral med följande ekvation i polära koordinater:
där a och b är parametrar som definierar spiralens inledande radie och avståndet mellan dess på varandra följande vändningar, där det senare är lika med 2 \pi b. Observera att en arkimedisk spiral ibland också kallas för en aritmetisk spiral. Detta namn härrör från den aritmetiska progressionen av avståndet från ursprunget till en punkt på samma radial.
Design av en parametriserad arkimedisk spiralgeometri
Nu när vi har introducerat arkimediska spiraler ska vi ta en titt på hur man parametriserar och skapar en sådan konstruktion för analys i COMSOL Multiphysics.
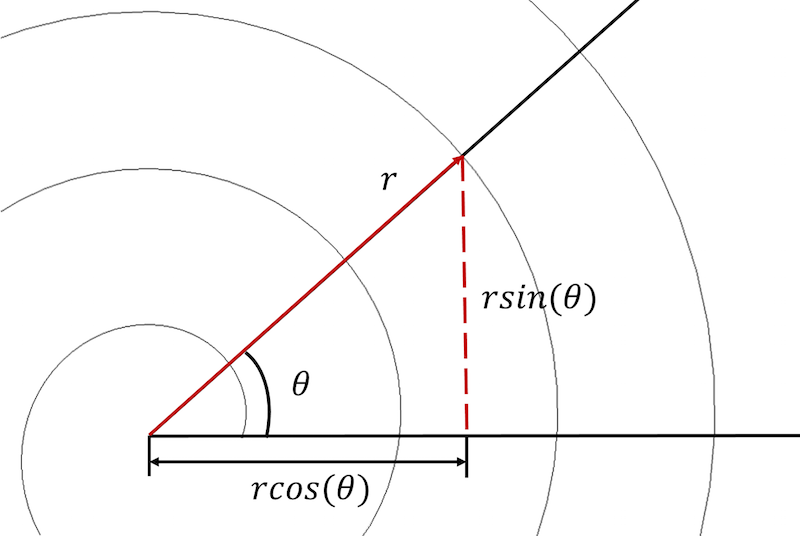
En arkimedisk spiral kan beskrivas i både polära och kartesiska koordinater.
För att börja måste vi konvertera spiralekvationerna från ett polärt till ett kartesianskt koordinatsystem och uttrycka varje ekvation i en parametrisk form:
x_{komponent}=rcos(\theta) \\
y_{komponent}=rsin(\theta)
\end{align*}
Denna omvandling gör det möjligt för oss att skriva om den arkimediska spiralens ekvation i en parametrisk form i det kartesiska koordinatsystemet:
x_{komponent}=(a+b\theta)cos(\theta) \\
y_{komponent}=(a+b\theta)sin(\theta)
\end{align*}
I COMSOL Multiphysics är det nödvändigt att bestämma vilka parametrar som ska definiera spiralgeometrin. Dessa parametrar är spiralens initiala radie a_{initial}, spiralens slutliga radie a_{final} och det önskade antalet varv n. Spiralens tillväxthastighet b kan sedan uttryckas som:
Fortsättningsvis måste vi besluta om spiralens startvinkel theta_0 och slutvinkel theta_f. Vi börjar med värdena theta_0=0 och theta_f=2 \pi n. Med denna information kan vi definiera en uppsättning parametrar för spiralgeometrin.
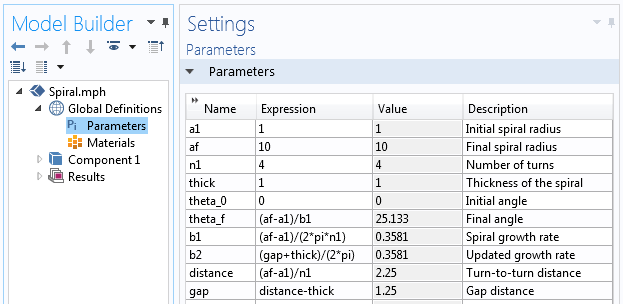
Parametrarna som används för att bygga spiralgeometrin.
För att bygga den här spiralen börjar vi med en 3D-komponent och skapar ett arbetsplan i grenen Geometri. I arbetsplanets geometri lägger vi sedan till en parametrisk kurva och använder de parametriska ekvationer som refereras ovan med en varierande vinkel för att rita en 2D-version av den arkimediska spiralen. Dessa ekvationer kan skrivas in direkt i den parametriska kurvans fält Expression, eller så kan vi först definiera varje ekvation i en ny analytisk funktion på följande sätt:
X_{fun}=(a+bs)cos(s) \\
Y_{fun}=(a+bs)sin(s) \\
\end{align*}
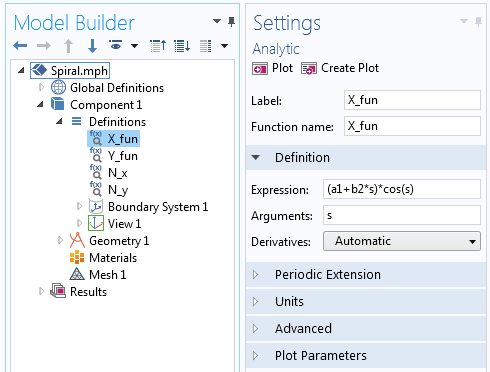
X-komponenten av den arkimediska spiralekvationen som definieras i den analytiska funktionen.
Den analytiska funktionen kan användas i uttrycken för den parametriska kurvan. I den här parametriska kurvan varierar vi parametern s från spiralens inledande vinkel, theta_0, till spiralens slutvinkel, theta_f=2 \pi n.
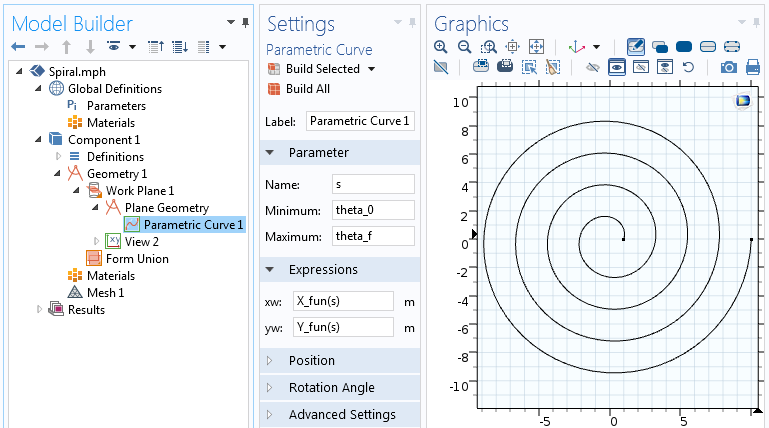
Inställningarna för funktionen Parametrisk kurva.
De parametriska spiralekvationer som används i funktionen Parametrisk kurva kommer att resultera i en spiral som representeras av en kurva. Låt oss nu bygga vidare på denna geometri och lägga till tjocklek till den för att skapa ett 2D-solidt objekt.
Hos denna punkt har vår spiral parametriserats i termer av den initiala radien a_{initial}, den slutliga radien a_{final} och det önskade antalet varv n. Nu måste vi införliva tjockleken som ytterligare en kontrollparameter i spiralekvationen.
Låt oss börja med spiralens huvudegenskap, som anger att avståndet mellan spiralens varv är lika med 2 \pi b. Detta är också likvärdigt med \frac{a_{final}-a_{initial}}{n}. För att införliva tjockleken representerar vi avståndet mellan varje på varandra följande spiralsväng som en summa av spiraltjockleken och det återstående gapet mellan svängarna, tjock+gap.
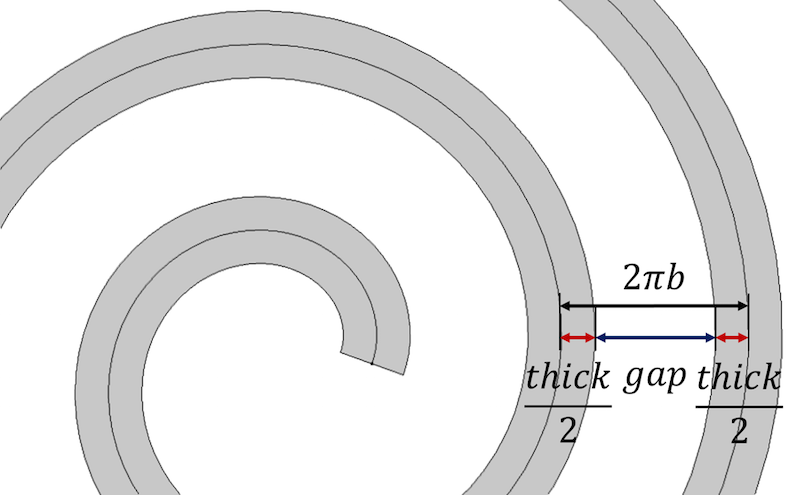
Avståndet mellan spiralsvängarna definieras i termer av spiraltjockleken och gapparametrarna.
För att kontrollera tjockleken och få identiskt avstånd mellan varven kan avståndet uttryckas som:
distance=\frac{a_{initial}-a_{final}}{n}} \\
gap=distance-thick
\end{align*}
Efter att ha definierat tjockleken och uttryckt gapet mellan varven i termer av tjocklek och konstant avstånd mellan spiralens centrumlinjer, kan vi skriva om spiralens tillväxtparameter i termer av tjocklek som:
distance=2\pi b \\
b=\frac{gap+tjocklek}{2\pi}
\end{align*}
Vi vill också uttrycka spiralens slutvinkel i termer av dess inledande och slutliga radier:
\theta_{final}=2 \pi n \\
a_{final}=\text{total distans}+a_{initial} \\
a_{final}=2 \pi bn+a_{initial} \\
n=\frac{a_{final}-a_{initial}}{2 \pi b} \\
\theta_{final}=\frac{2 \pi (a_{final}-a_{initial})}{2 \pi b} \\
\theta_{final}=\frac{a_{final}-a_{initial}}}{b}
\end{align*}
Vill du starta spiralen från en annan vinkel än noll? I så fall måste du lägga till denna initiala vinkel till din slutliga vinkel i uttrycket för parametern: theta_f=\frac{a_{final}-a_{initial}}}{b}+theta_0.
Duplicera den befintliga spiralkurvan två gånger och placera dessa kurvor med en förskjutning på -\frac{thick}{2} och +\frac{thick}{2} med avseende på den initiala spiralkurvan gör det möjligt för oss att bygga spiralen med tjocklek. För att placera de övre och undre spiralerna korrekt måste vi se till att de förskjutna spiralerna är normala i förhållande till den ursprungliga spiralkurvan. Detta kan uppnås genom att multiplicera förskjutningsavståndet \pm\frac{thick}{2} med en enhetsvektor som är normal till spiralkurvan. Ekvationerna för normalvektorerna till en kurva i parametrisk form är:
där s är den parameter som används i funktionen Parametrisk kurva. För att få en enhetsnormal måste vi dela dessa uttryck med normalens längd:
Våra uppdaterade parametriska ekvationer för den arkimediska spiralen med en halvtjockleksförskjutning är:
x_{component}=(a+bs)cos(s)-\frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}\frac{thick}{2} \\
y_{komponent}=(a+bs)sin(s)+\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}}\frac{thick}{2}
\end{align*}
Att skriva ut dessa ekvationer i den parametriska kurvans uttrycksfält kan vara ganska tidsödande. Därför introducerar vi följande notation:
N_x=-\frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}} \\
N_y=\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2 }}
\end{align*}
där varje N_x och N_y definieras via den analytiska funktionen i COMSOL Multiphysics, på samma sätt som vi definierade X_{fun} och Y_{fun} för den första parametriska kurvan. I funktionen använder vi differentieringsoperatorn d(f(x),x) för att ta derivatan, vilket visas i följande skärmdump.
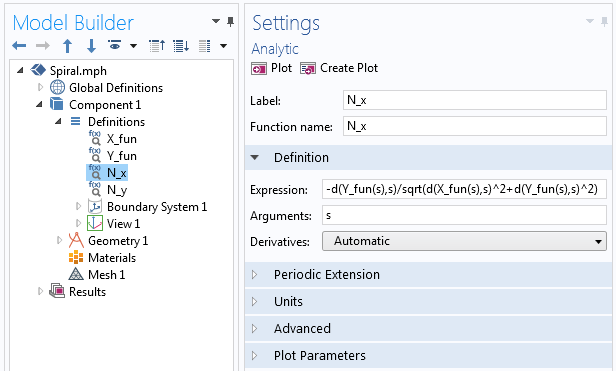
Exempel på derivatoroperatorn som används i den analytiska funktionen.
Funktionerna X_{fun}, Y_{fun}, N_x och N_y kan sedan användas direkt i den parametriska kurvans uttryck för kurvan på ena sidan:
x_{lower}=X_{fun}(s)+N_x(s)\frac{thick}{2} \\
y_{lower}=Y_{fun}(s)+N_y(s)\frac{thick}{2}
\end{align*}
Funktionerna kan också användas för kurvan på andra sidan:
x_{upper}=X_{fun}(s)-N_x(s)\frac{thick}{2} \\
y_{upper}=Y_{fun}(s)-N_y(s)\frac{thick}{2}
\end{align*}
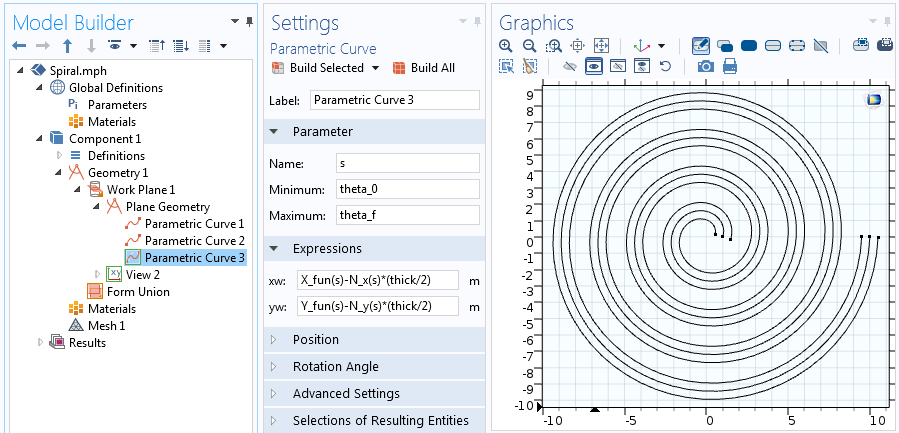
Ekvationer för den andra av de två förskjutna parametriska kurvorna.
För att sammanfoga ändarna av två kurvor lägger vi till ytterligare två parametriska kurvor med hjälp av en liten modifiering av ekvationerna ovan. För den kurva som ansluter till spiralens centrum måste vi utvärdera X_{fun}, Y_{fun}, N_x och N_y för startvärdet av vinkeln, theta. För kurvan som ansluter till spiralens yttre sida måste vi utvärdera slutvärdet för theta. Därför är den sammanfogande kurvan i mitten:
X_{fun}(theta_0)+s\cdot N_x(theta_0)\cdot\frac{thick}{2} \\
Y_{fun}(theta_0)+s\cdot N_y(theta_0)\cdot\frac{thick}{2}
\end{align*}
Den yttre sammanfogande kurvan är under tiden:
X_{fun}(theta_f)+s\cdot N_x(theta_f)\cdot\frac{thick}{2} \\
Y_{fun}(theta_f)+s\cdot N_y(theta_f)\cdot\frac{thick}{2}
\end{align*}
I båda ovanstående ekvationer går s från -1 till +1, vilket visas i skärmdumpen nedan.
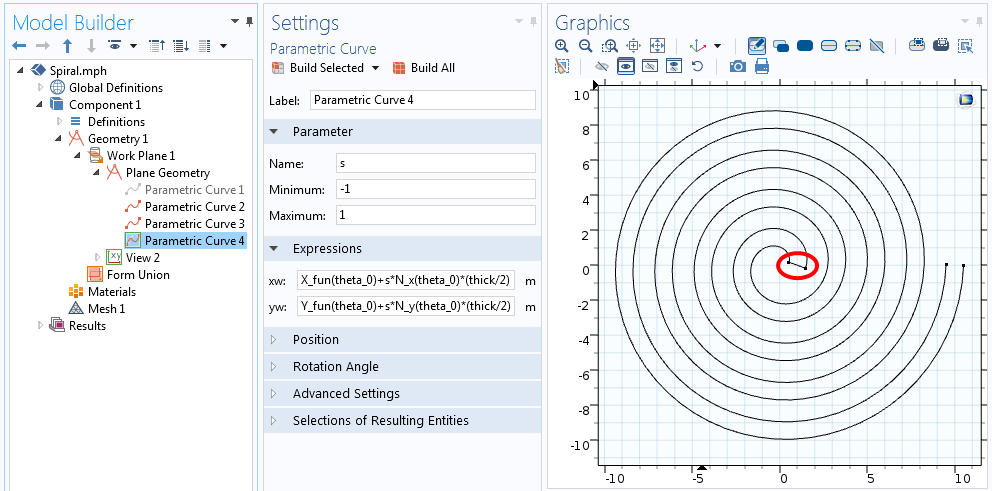
Ekvationer för kurvan som ansluter till spiralens ena ände.
Vi har nu fem kurvor som definierar spiralens mittlinje och alla fyra sidor av profilen. Vi kan inaktivera (eller till och med ta bort) kurvan som beskriver mittlinjen eftersom den inte är riktigt nödvändig, så att bara spiralens kontur kvarstår. Med konturerna av vår spiral definierade kan operationen Convert to Solid användas för att skapa ett enda geometriskt objekt. Denna 2D-spiral kan slutligen extruderas till 3D via operationen Extrude.
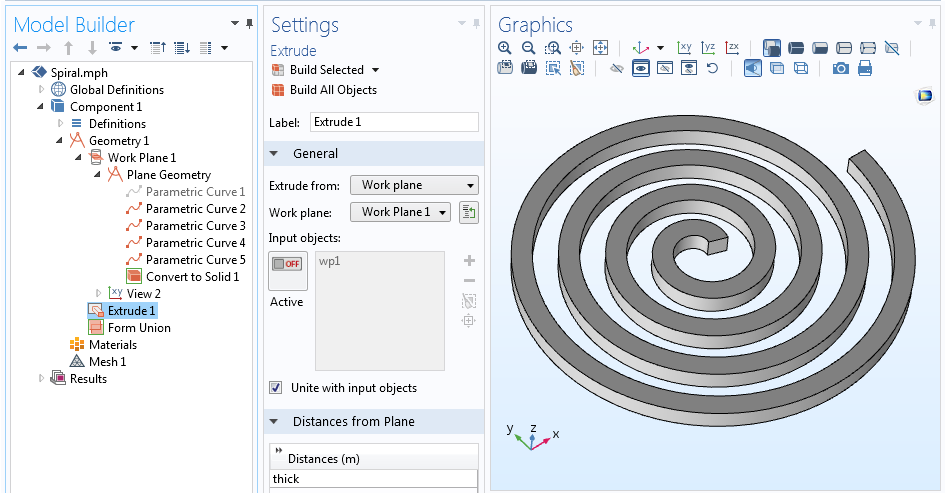
Den fullständiga geometrisekvensen och den extruderade 3D-spiralgeometrin.
Avslutande anmärkningar om modellering av arkimediska spiraler i COMSOL Multiphysics
Vi har gått igenom stegen för att skapa en fullt parametriserad arkimedisk spiral. Med denna spiralgeometri kan du ändra någon av parametrarna och experimentera med olika konstruktioner, eller till och med använda dem som parametrar i en optimeringsstudie. Vi uppmuntrar dig att använda den här tekniken i dina egna modelleringsprocesser för att främja analysen av just din spiralbaserade tekniska konstruktion.