Las espirales de Arquímedes se utilizan a menudo en el análisis de bobinas inductoras, intercambiadores de calor en espiral y dispositivos microfluídicos. Hoy demostraremos cómo construir una espiral de Arquímedes utilizando ecuaciones analíticas y sus derivadas para definir un conjunto de curvas en espiral. Basándonos en estas curvas, crearemos una geometría 2D con un grosor específico, extruyéndola a una geometría 3D completa.
Una breve introducción a las espirales de Arquímedes
Ampliamente observadas en la naturaleza, las espirales, o hélices, se utilizan en muchos diseños de ingeniería. Como ingeniero eléctrico, por ejemplo, puede enrollar bobinas inductivas en patrones espirales y diseñar antenas helicoidales. Como ingeniero mecánico, puede utilizar espirales en el diseño de muelles, engranajes helicoidales o incluso en el mecanismo de reloj que se muestra a continuación.

Un ejemplo de espiral de Arquímedes utilizada en el mecanismo de un reloj. Imagen de Greubel Forsey. Con licencia CC BY-SA 3.0, vía Wikimedia Commons.
Aquí nos centraremos en un tipo específico de espiral, la que aparece en el mecanismo mostrado arriba: una espiral de Arquímedes. Una espiral de Arquímedes es un tipo de espiral que tiene una distancia fija entre sus vueltas sucesivas. Esta propiedad le permite ser ampliamente utilizada en el diseño de bobinas y muelles planos.
Podemos describir una espiral de Arquímedes con la siguiente ecuación en coordenadas polares:
donde a y b son parámetros que definen el radio inicial de la espiral y la distancia entre sus vueltas sucesivas, siendo esta última igual a 2 \pi b. Obsérvese que una espiral de Arquímedes también se denomina a veces espiral aritmética. Este nombre deriva de la progresión aritmética de la distancia desde el origen hasta el punto del mismo radial.
Diseño de una geometría de espiral arquimédica parametrizada
Ahora que hemos introducido las espirales arquimédicas, veamos cómo parametrizar y crear un diseño de este tipo para su análisis en COMSOL Multiphysics.
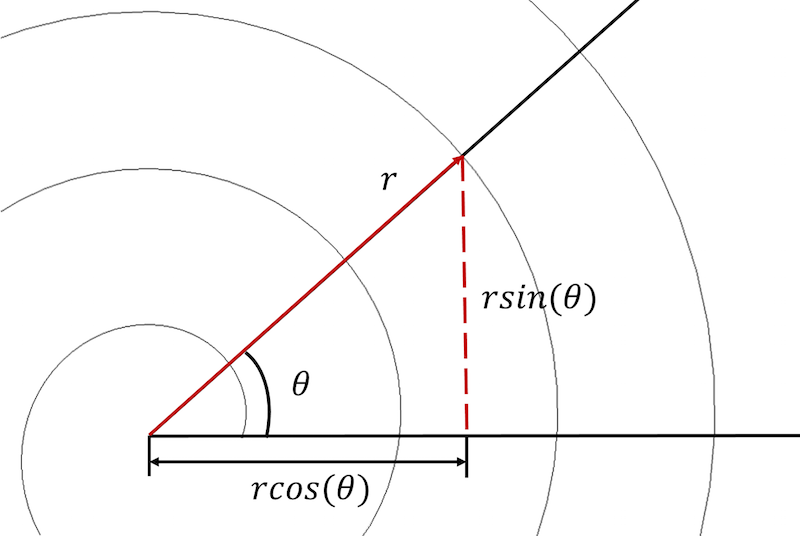
Una espiral arquimediana puede describirse tanto en coordenadas polares como cartesianas.
Para empezar, necesitamos convertir las ecuaciones de la espiral de un sistema de coordenadas polares a un sistema de coordenadas cartesianas y expresar cada ecuación en forma paramétrica:
x_{componente}=rcos(\theta) \
y_{componente}=rsin(\theta)
{final{align*}
Esta transformación nos permite reescribir la ecuación de la espiral de Arquímedes en una forma paramétrica en el sistema de coordenadas cartesianas:
x_{componente}=(a+b\theta)cos(\theta) {5931>y_{componente}=(a+b\theta)sin(\theta)
{fin{align*}
En COMSOL Multiphysics, es necesario decidir el conjunto de parámetros que definirán la geometría de la espiral. Estos parámetros son el radio inicial de la espiral a_{inicial}, el radio final de la espiral a_{final}, y el número deseado de vueltas n. La tasa de crecimiento de la espiral b puede entonces expresarse como:
Además, necesitamos decidir el ángulo inicial de la espiral theta_0 y el ángulo final theta_f. Comencemos con los valores de theta_0=0 y theta_f=2 \pi n. Con esta información, podemos definir un conjunto de parámetros para la geometría de la espiral.
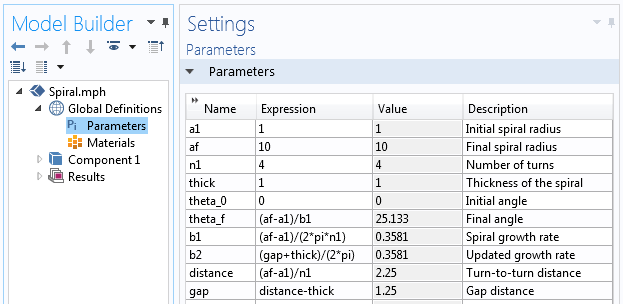
Los parámetros utilizados para construir la geometría de la espiral.
Para construir esta espiral, comenzaremos con un Componente 3D y crearemos un Plano de Trabajo en la rama Geometría. En la geometría del Plano de Trabajo, añadimos entonces una Curva Paramétrica y utilizamos las ecuaciones paramétricas referenciadas anteriormente con un ángulo variable para dibujar una versión 2D de la espiral de Arquímedes. Estas ecuaciones pueden ser introducidas directamente en el campo Expresión de la curva paramétrica, o podemos definir primero cada ecuación en una nueva función Analítica como
X_{fun}=(a+bs)cos(s) \
Y_{fun}=(a+bs)sin(s) \
{final{align*}
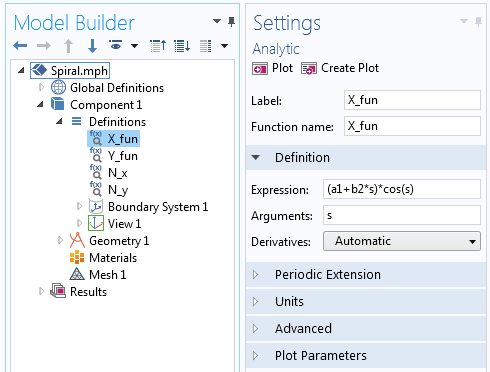
El componente X de la ecuación de la espiral de Arquímedes definida en la función Analítica.
La función Analítica se puede utilizar en las expresiones de la Curva Paramétrica. En esta Curva Paramétrica, variamos el parámetro s desde el ángulo inicial de la espiral, theta_0, hasta el ángulo final de la espiral, theta_f=2 \pi n.
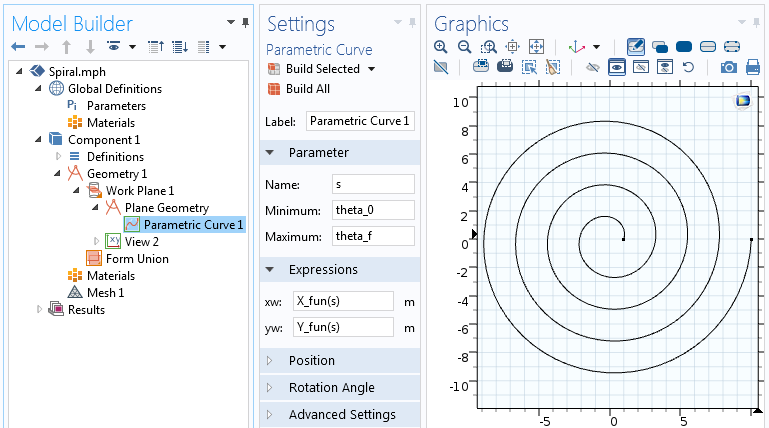
Los ajustes de la función Curva Paramétrica.
Las ecuaciones de la espiral paramétrica utilizadas en la función Curva Paramétrica darán como resultado una espiral representada por una curva. Construyamos ahora sobre esta geometría, añadiéndole grosor para crear un objeto sólido 2D.
Hasta este punto, nuestra espiral ha sido parametrizada en términos del radio inicial a_{inicial}, el radio final a_{final}, y el número deseado de vueltas n. Ahora, debemos incorporar el espesor como otro parámetro de control en la ecuación de la espiral.
Comencemos con la propiedad principal de la espiral, que establece que la distancia entre las vueltas de la espiral es igual a 2 \pi b. Esto también es equivalente a \frac{a_{final}-a_{inicial}{n}. Para incorporar el grosor, representamos la distancia entre cada vuelta sucesiva de la espiral como una suma del grosor de la espiral y el hueco restante entre las vueltas, thick+gap.
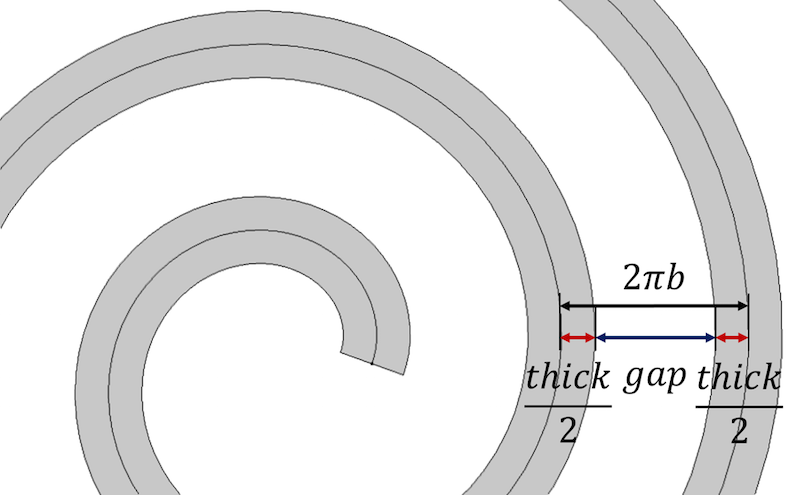
La distancia entre las vueltas de la espiral se define en términos de los parámetros de grosor y hueco de la espiral.
Para controlar el grosor y obtener una distancia idéntica entre las espiras, la distancia puede expresarse como:
distancia={frac{a_{inicial}-a_{final}{n} \
gap=distancia-espesor
\end{align*}
Después de definir el espesor y expresar el gap entre vueltas en términos de espesor y distancia constante entre líneas centrales de la espiral, podemos reescribir el parámetro de crecimiento de la espiral en términos de espesor como:
distancia=2\pi b \\\\\N-
b=\frac{gap+espesor}{2\pi}
{final{alinear*}
También querremos expresar el ángulo final de la espiral en términos de sus radios inicial y final:
{theta_{final}=2 \pi n \
a_{final}={texto}{distancia total}+a_{inicial}}. \\
¿Quieres empezar la espiral desde un ángulo distinto de cero? Si es así, tendrá que añadir este ángulo inicial a su ángulo final en la expresión del parámetro: theta_f=\frac{a_{final}-a_{inicial}{b}+theta_0.
Duplicar la curva de la espiral existente dos veces y colocar estas curvas con un desfase de -\frac{grueso}{2} y +\frac{grueso}{2} respecto a la curva de la espiral inicial nos permite construir la espiral con espesor. Para posicionar correctamente las espirales superior e inferior, debemos asegurarnos de que las espirales desplazadas son normales a la curva de la espiral inicial. Esto puede lograrse multiplicando la distancia de desplazamiento \pm\frac{espesor}{2} por el vector unitario normal a la curva espiral. Las ecuaciones de los vectores normales a una curva en forma paramétrica son:
donde s es el parámetro utilizado en la función Curva Paramétrica. Para obtener una normal unitaria, necesitamos dividir estas expresiones por la longitud de la normal:
Nuestras ecuaciones paramétricas actualizadas para la espiral de Arquímedes con un desplazamiento de medio grosor son:
x_{component}=(a+bs)cos(s)-\frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}\frac{thick}{2} \\
Escribir estas ecuaciones en los campos de expresión de la curva paramétrica puede llevar bastante tiempo. Por lo tanto, introducimos la siguiente notación:
N_y=\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2 }}
\end{align*}
donde cada N_x y N_y se define a través de la función Analytic en COMSOL Multiphysics, de forma similar a como definimos X_{fun} e Y_{fun} para la primera curva paramétrica. Dentro de la función, utilizamos el operador de diferenciación, d(f(x),x), para tomar la derivada, como se representa en la siguiente captura de pantalla.
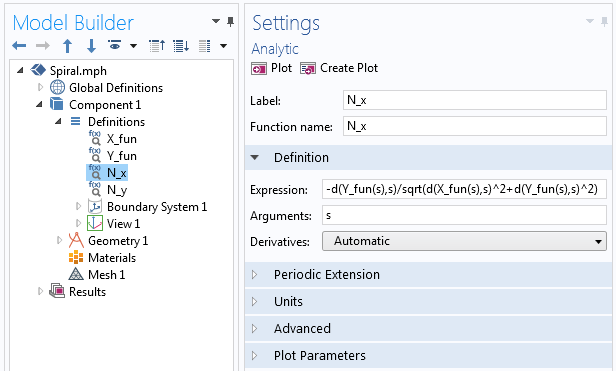
Ejemplos del operador de derivación utilizado en la función Analytic.
Las funciones X_{fun}, Y_{fun}, N_x, y N_y pueden entonces usarse directamente en las expresiones de la curva paramétrica para la curva de un lado:
x_{inferior}=X_{fun}(s)+N_x(s)\frac{espesor}{2} \\
y_{lower}=Y_{fun}(s)+N_y(s)\frac{thick}{2}
\end{align*}
Las funciones también pueden usarse para la curva del otro lado:
x_{superior}=X_{fun}(s)-N_x(s)\frac{espesor}{2} \5931>y_{superior}=Y_{fun}(s)-N_y(s)\frac{espesor}{2}
{end{align*}
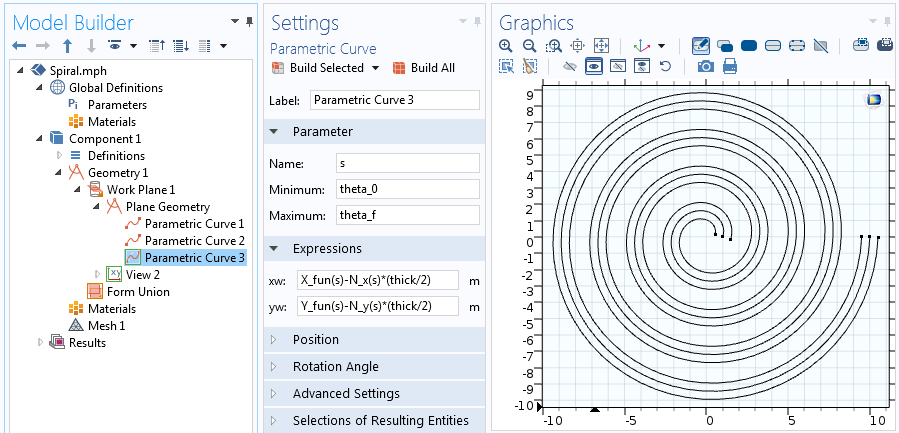
Cuestiones para la segunda de las dos curvas paramétricas desplazadas.
Para unir los extremos de dos curvas, añadimos dos curvas paramétricas más utilizando una ligera modificación de las ecuaciones mencionadas anteriormente. Para la curva que une el centro de la espiral, tenemos que evaluar X_{fun}, Y_{fun}, N_x, y N_y para el valor inicial del ángulo, theta. Para la curva que une el lado exterior de la espiral, tenemos que evaluar el valor final de theta. Por lo tanto, la curva de unión en el centro es:
X_{fun}(theta_0)+s\cdot N_x(theta_0)\cdot{frac}{2} \\
Y_{fun}(theta_0)+s\cdot N_y(theta_0)\cdot\frac{thick}{2}
\end{align*}
La curva de unión exterior, por su parte, es:
X_{fun}(theta_f)+s\cdot N_x(theta_f)\cdot{frac{espesor}{2} \\
Y_{fun}(theta_f)+s\cdot N_y(theta_f)\cdot\frac{thick}{2}
\end{align*}
En ambas ecuaciones anteriores, s va de -1 a +1, como se muestra en la captura de pantalla de abajo.
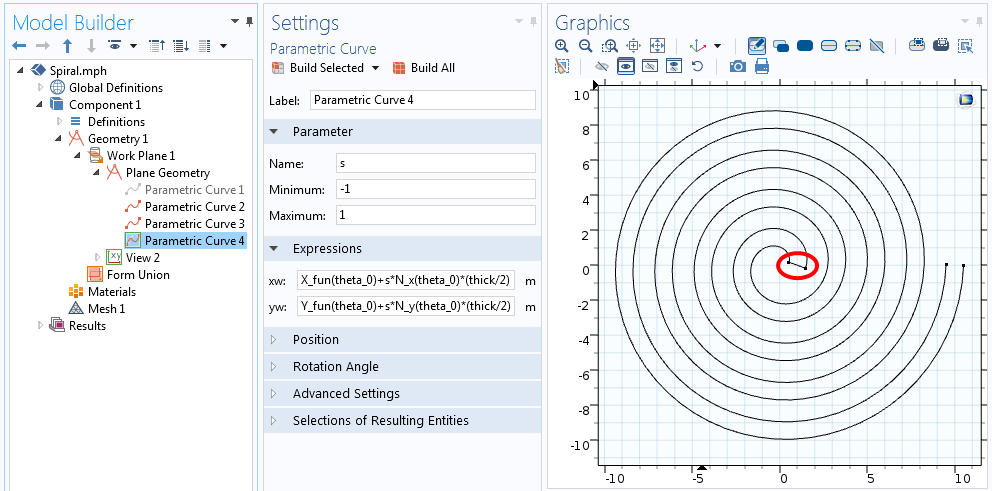
Ecuaciones para la curva que une un extremo de la espiral.
Ahora tenemos cinco curvas que definen la línea central de la espiral y los cuatro lados del perfil. Podemos desactivar (o incluso eliminar) la curva que describe la línea central ya que no es realmente necesaria, dejando sólo el contorno de la espiral. Con el contorno de nuestra espiral definido, se puede utilizar la operación Convertir en sólido para crear un único objeto geométrico. Esta espiral 2D puede finalmente ser extruida en 3D a través de la operación Extrude.
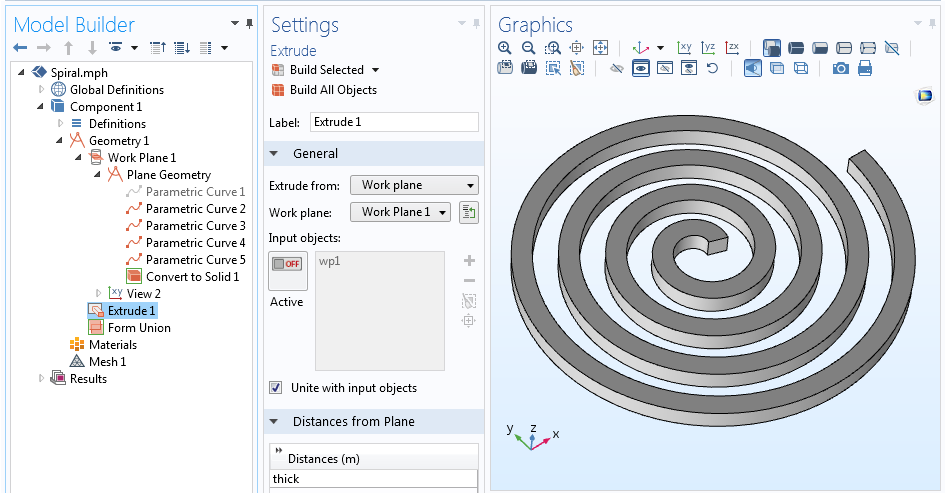
La secuencia geométrica completa y la geometría de la espiral 3D extruida.
Observaciones finales sobre el modelado de espirales de Arquímedes en COMSOL Multiphysics
Le hemos guiado a través de los pasos para crear una espiral de Arquímedes totalmente parametrizada. Con esta geometría de espiral, puede cambiar cualquiera de los parámetros y experimentar con diferentes diseños, o incluso utilizarlos como parámetros en un estudio de optimización. Le animamos a utilizar esta técnica en sus propios procesos de modelado, avanzando en el análisis de su diseño particular de ingeniería basado en la espiral.