Le spirali archimedee sono spesso usate nell’analisi di bobine di induttori, scambiatori di calore a spirale e dispositivi microfluidici. Oggi dimostreremo come costruire una spirale archimedea usando equazioni analitiche e le loro derivate per definire un insieme di curve a spirale. Sulla base di queste curve, creeremo poi una geometria 2D con spessore specifico, estrudendola in una geometria 3D completa.
Breve introduzione alle spirali archimedee
Si osservano ampiamente in natura, le spirali, o eliche, sono utilizzate in molti progetti di ingegneria. Come ingegnere elettrico, per esempio, si possono avvolgere bobine induttive in modelli a spirale e progettare antenne elicoidali. Come ingegnere meccanico, puoi usare le spirali quando progetti molle, ingranaggi elicoidali, o anche il meccanismo dell’orologio evidenziato qui sotto.

Un esempio di spirale archimedea usata in un meccanismo di orologio. Immagine di Greubel Forsey. Licensed by CC BY-SA 3.0, via Wikimedia Commons.
Qui ci concentreremo su un tipo specifico di spirale, quella che è presente nel meccanismo mostrato sopra: una spirale archimedea. Una spirale archimedea è un tipo di spirale che ha una distanza fissa tra i suoi giri successivi. Questa proprietà le permette di essere ampiamente utilizzata nella progettazione di bobine piane e molle.
Possiamo descrivere una spirale archimedea con la seguente equazione in coordinate polari:
dove a e b sono parametri che definiscono il raggio iniziale della spirale e la distanza tra le sue spire successive, quest’ultima uguale a 2 \pi b. Si noti che una spirale archimedea è anche talvolta chiamata spirale aritmetica. Questo nome deriva dalla progressione aritmetica della distanza dall’origine al punto sulla stessa radiale.
Progettazione di una geometria a spirale archimedea parametrizzata
Ora che abbiamo introdotto le spirali archimedee, diamo uno sguardo a come parametrizzare e creare un tale disegno per l’analisi in COMSOL Multiphysics.
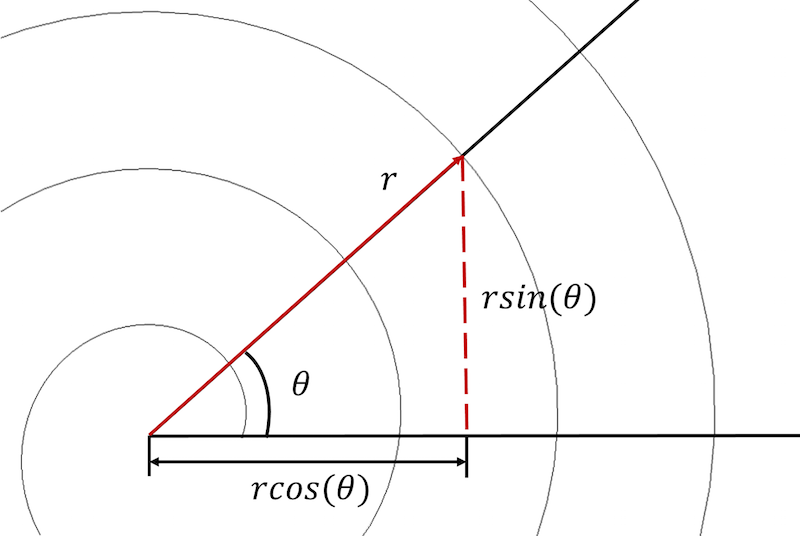
Una spirale archimedea può essere descritta sia in coordinate polari che cartesiane.
Per iniziare, abbiamo bisogno di convertire le equazioni della spirale da un sistema di coordinate polari a uno cartesiano ed esprimere ogni equazione in forma parametrica:
x_componente}=rcos(\theta) \\5931>y_componente}=rsin(\theta)
fine{align*}
Questa trasformazione ci permette di riscrivere l’equazione della spirale archimedea in forma parametrica nel sistema di coordinate cartesiane:
x_componente}=(a+b\theta)cos(\theta) \
y_componente}=(a+b\theta)sin(\theta)
fine{align*}
In COMSOL Multiphysics, è necessario decidere l’insieme dei parametri che definiranno la geometria della spirale. Questi parametri sono il raggio iniziale a_iniziale della spirale, il raggio finale a_finale della spirale e il numero desiderato di giri n. Il tasso di crescita della spirale b può quindi essere espresso come:
Inoltre, dobbiamo decidere l’angolo iniziale theta_0 e l’angolo finale theta_f della spirale. Cominciamo con i valori di theta_0=0 e theta_f=2 \pi n. Con queste informazioni, siamo in grado di definire una serie di parametri per la geometria della spirale.
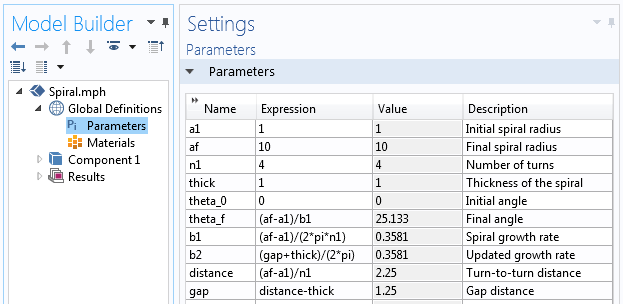
I parametri utilizzati per costruire la geometria della spirale.
Per costruire questa spirale, cominceremo con un componente 3D e creeremo un piano di lavoro nel ramo Geometry. Nella geometria del Piano di lavoro, aggiungiamo poi una Curva parametrica e usiamo le equazioni parametriche di cui sopra con un angolo variabile per disegnare una versione 2D della spirale archimedea. Queste equazioni possono essere inserite direttamente nel campo Expression della curva parametrica, oppure possiamo prima definire ogni equazione in una nuova funzione Analytic come:
X_{fun}=(a+bs)cos(s) \\
Y_{fun}=(a+bs)sin(s) \
fine{align*}
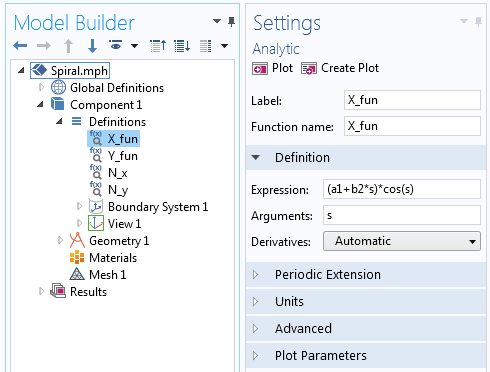
La componente X dell’equazione della spirale archimedea definita nella funzione Analytic.
La funzione analitica può essere usata nelle espressioni della curva parametrica. In questa Curva Parametrica, varieremo il parametro s dall’angolo iniziale della spirale, theta_0, all’angolo finale della spirale, theta_f=2 \pi n.
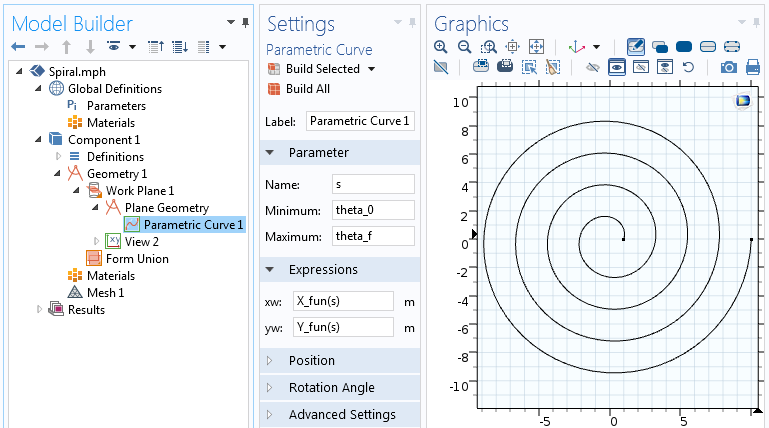
Le impostazioni della funzione Curva Parametrica.
Le equazioni della spirale parametrica usate nella funzione Curva Parametrica risulteranno in una spirale rappresentata da una curva. Costruiamo ora su questa geometria, aggiungendovi lo spessore per creare un oggetto solido 2D.
Fino a questo punto, la nostra spirale è stata parametrizzata in termini di raggio iniziale a_{iniziale}, raggio finale a_{finale}, e numero di giri desiderato n. Ora, dobbiamo incorporare lo spessore come un altro parametro di controllo nell’equazione della spirale.
Iniziamo con la proprietà principale della spirale, che afferma che la distanza tra i giri della spirale è uguale a 2 \pi b. Questo è anche equivalente a \frac{a_{finale}-a_{iniziale}}{n}. Per incorporare lo spessore, rappresentiamo la distanza tra ogni giro successivo della spirale come somma dello spessore della spirale e dello spazio rimanente tra i giri, spessore+gap.
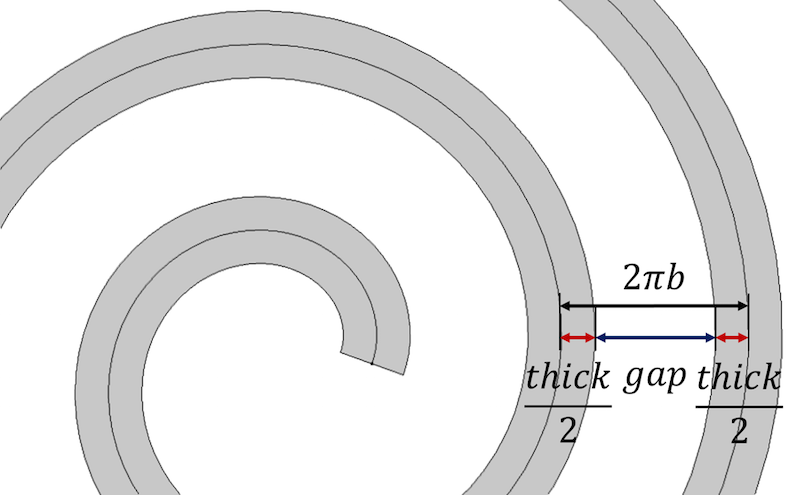
La distanza tra i giri della spirale è definita in termini dei parametri dello spessore della spirale e dello spazio.
Per controllare lo spessore e ottenere una distanza identica tra le spire, la distanza può essere espressa come:
distanza=frac{a_initial}-a_{final}}{n} \\
distanza=2\pi b \\5931>b=frac{gap+spessore}{2\pi}
fine{align*}
Vorremo anche esprimere l’angolo finale della spirale in termini dei suoi raggi iniziale e finale:
{theta_finale}=2 \pi n \\5931>a_finale}=={ distanza totale}+a_iniziale} \
a_finale}=2 \pi bn+a_iniziale} \5931>n=frac{a_finale}-a_iniziale}{2 \pi b} \5931>theta_{finale}=frac{2 \pi (a_finale}-a_iniziale})}{2 \pi b} \5931>theta_{finale}=frac{a_finale}-a_iniziale}{b}
fine{align*}
Vuoi iniziare la spirale da un angolo diverso da zero? Se è così, dovrai aggiungere questo angolo iniziale al tuo angolo finale nell’espressione per il parametro: theta_f=\frac{a_{finale}-a_{iniziale}}{b}+theta_0.
Duplicando due volte la curva a spirale esistente e posizionando queste curve con un offset di -\frac{ spessore}{2} e +\frac{ spessore}{2} rispetto alla curva a spirale iniziale ci permette di costruire la spirale con spessore. Per posizionare correttamente le spirali superiori e inferiori, dobbiamo assicurarci che le spirali di offset siano normali alla curva a spirale iniziale. Questo può essere ottenuto moltiplicando la distanza di offset \pm\frac{spessore}{2} per il vettore unitario normale alla curva della spirale. Le equazioni dei vettori normali ad una curva in forma parametrica sono:
dove s è il parametro usato nella funzione Curva Parametrica. Per ottenere una normale unitaria, dobbiamo dividere queste espressioni per la lunghezza della normale:
Le nostre equazioni parametriche aggiornate per la spirale archimedea con uno spostamento di metà spessore sono:
x_{component}=(a+bs)cos(s)-\frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}\frac{thick}{2} \
y_{componente}=(a+bs)sin(s)+\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}{frac{thick}{2}
{align*}
Scrivere queste equazioni nei campi di espressione della curva parametrica può richiedere molto tempo. Per questo motivo, introduciamo la seguente notazione:
N_x=–frac{dy/ds}{sqrt{(dx/ds)^2+(dy/ds)^2} \\
N_y=\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2 }}
\end{align*}
dove ogni N_x e N_y è definito tramite la funzione Analytic in COMSOL Multiphysics, simile a come abbiamo definito X_{fun} e Y_{fun} per la prima curva parametrica. All’interno della funzione, usiamo l’operatore di differenziazione, d(f(x),x), per prendere la derivata, come illustrato nella seguente schermata.
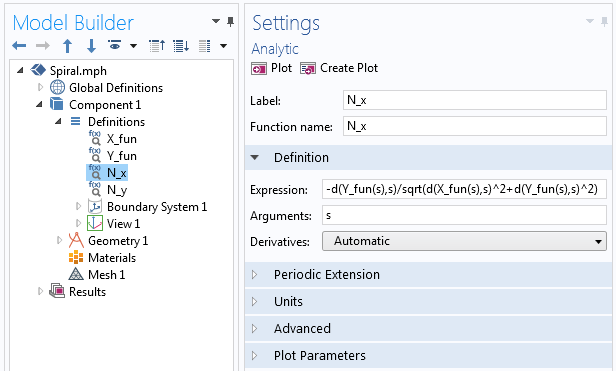
Esempi dell’operatore di derivazione usato nella funzione Analytic.
Le funzioni X_{fun}, Y_{fun}, N_x e N_y possono quindi essere utilizzate direttamente nelle espressioni della curva parametrica per la curva su un lato:
x_{lower}=X_{fun}(s)+N_x(s)\frac{thick}{2} \\
y_{lower}=Y_{fun}(s)+N_y(s)\frac{thick}{2}
\end{align*}
Le funzioni possono essere usate anche per la curva dall’altra parte:
x_{upper}=X_{fun}(s)-N_x(s)\frac{thick}{2}
y_{upper}=Y_{fun}(s)-N_y(s)\frac{thick}{2}
Fine{align*}
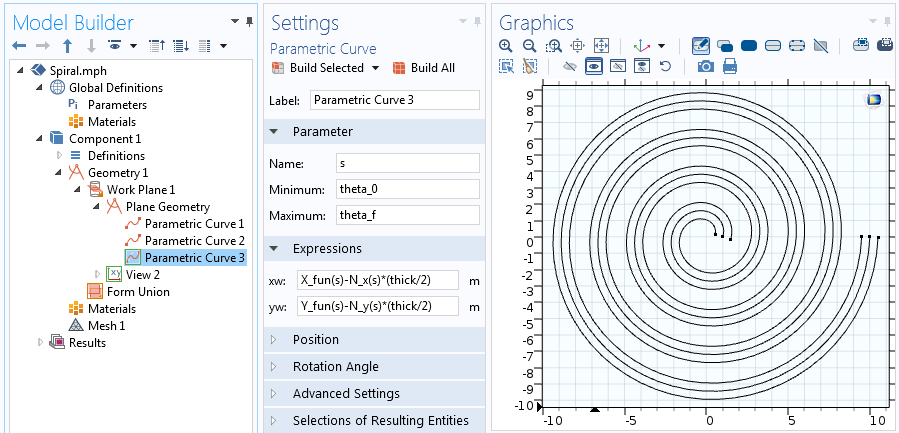
Equazioni per la seconda delle due curve parametriche offset.
Per unire le estremità di due curve, aggiungiamo altre due curve parametriche usando una leggera modifica delle equazioni menzionate sopra. Per la curva che unisce il centro della spirale, dobbiamo valutare X_{fun}, Y_{fun}, N_x e N_y per il valore iniziale dell’angolo, theta. Per la curva che unisce il lato esterno della spirale, dobbiamo valutare il valore finale di theta. Pertanto, la curva di unione al centro è:
X_{fun}(theta_0)+s\cdot N_x(theta_0)\cdotfrac{2} \\
Y_{fun}(theta_0)+s\cdot N_y(theta_0)\cdot\frac{thick}{2}
\end{align*}
La curva di unione esterna, invece, è:
X_{fun}(theta_f)+s\cdot N_x(theta_f)\cdotfrac{thick}{2} \\
Y_{fun}(theta_f)+s\cdot N_y(theta_f)\cdot\frac{thick}{2}
\end{align*}
In entrambe le equazioni di cui sopra, s va da -1 a +1, come mostrato nello screenshot qui sotto.
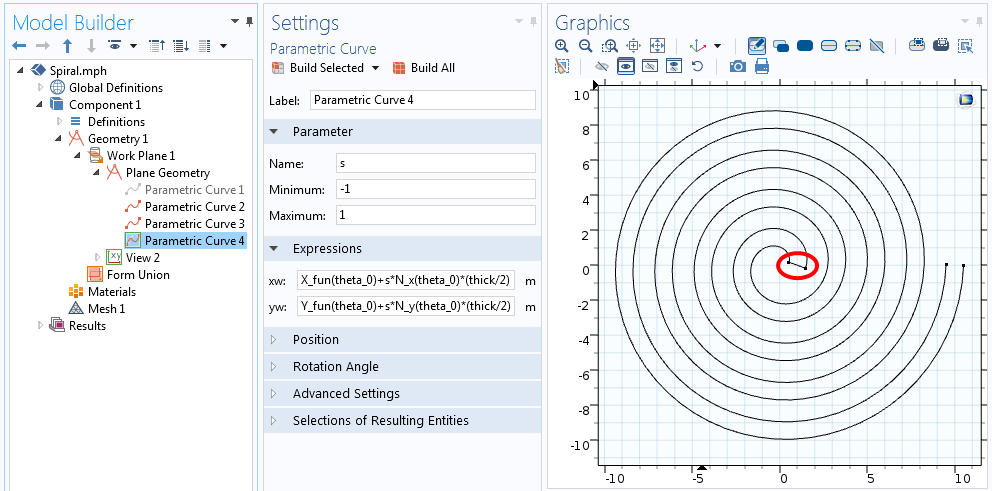
Equazioni per la curva che unisce un’estremità della spirale.
Ora abbiamo cinque curve che definiscono la linea centrale della spirale e tutti e quattro i lati del profilo. Possiamo disabilitare (o anche cancellare) la curva che descrive la linea centrale, poiché non è veramente necessaria, lasciando solo il contorno della spirale. Con il contorno della nostra spirale definito, l’operazione Convert to Solid può essere usata per creare un singolo oggetto geometrico. Questa spirale 2D può infine essere estrusa in 3D tramite l’operazione Extrude.
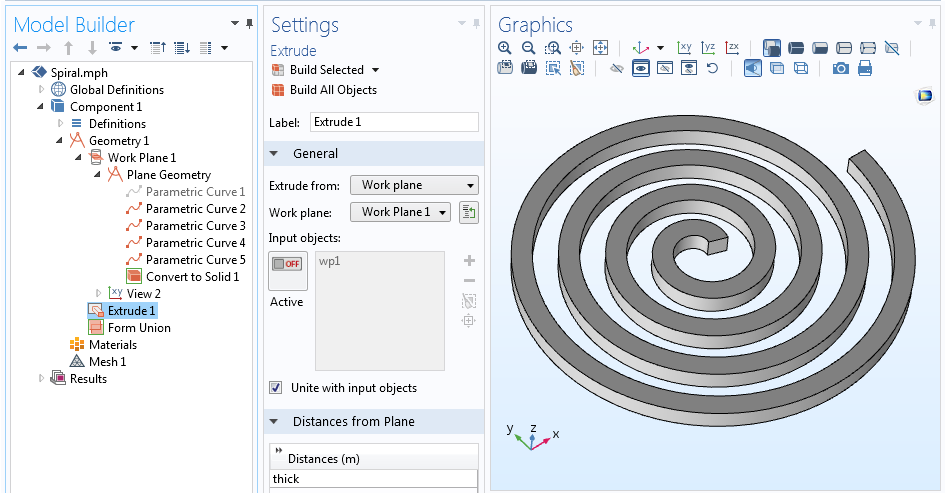
La sequenza geometrica completa e la geometria della spirale estrusa in 3D.
Raccomandazioni conclusive sulla modellazione di spirali archimedee in COMSOL Multiphysics
Abbiamo seguito i passi per la creazione di una spirale archimedea completamente parametrizzata. Con questa geometria a spirale, potete cambiare qualsiasi parametro e sperimentare diversi disegni, o anche usarli come parametri in uno studio di ottimizzazione. Vi incoraggiamo ad utilizzare questa tecnica nei vostri processi di modellazione, facendo progredire l’analisi del vostro particolare progetto di ingegneria basato sulla spirale.