Macierz to tablica liczb:

Macierz
(ta ma 2 wiersze i 3 kolumny)
Mnożenie macierzy przez pojedynczą liczbę jest proste:
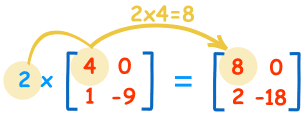
| 2×4=8 | 2×0=0 |
| 2×1=2 | 2×-9=-18 |
Liczbę („2” w tym przypadku) nazywamy skalarem, więc jest to tzw. mnożenie skalarne.
Mnożenie macierzy przez inną macierz
Ale aby pomnożyć macierz przez inną macierz musimy wykonać „iloczyn kropkowy” wierszy i kolumn … co to oznacza? Zobaczmy na przykładzie:
Aby obliczyć odpowiedź dla 1. wiersza i 1. kolumny:
„Iloczyn kropkowy” polega na mnożeniu odpowiadających sobie elementów, a następnie sumowaniu:
(1, 2, 3) – (7, 9, 11) = 1×7 + 2×9 + 3×11
= 58
Dopasowujemy 1. człony (1 i 7), mnożymy je, podobnie dla 2. członów (2 i 9) oraz 3. członów (3 i 11), a na koniec sumujemy.
Chcesz zobaczyć inny przykład? Oto on dla 1. rzędu i 2. kolumny:
(1, 2, 3) – (8, 10, 12) = 1×8 + 2×10 + 3×12
= 64
To samo możemy zrobić dla 2. rzędu i 1. kolumny:
(4, 5, 6) – (7, 9, 11) = 4×7 + 5×9 + 6×11
= 139
A dla 2. wiersza i 2. kolumny:
(4, 5, 6) – (8, 10, 12) = 4×8 + 5×10 + 6×12
= 154
I otrzymujemy:
DONE!
Why Do It This Way?
Ten sposób mnożenia może wydawać się dziwny i skomplikowany, ale jest konieczny!
Mogę podać przykład z życia wzięty, aby zilustrować, dlaczego mnożymy macierze w ten sposób.
Przykład: Lokalny sklep sprzedaje 3 rodzaje placków.
- Placki z jabłkami kosztują po 3$
- Placki z wiśniami kosztują po 4$
- Placki z jagodami kosztują po 2$
A oto ile sprzedali w ciągu 4 dni:
Teraz pomyśl o tym …. wartość sprzedaży dla poniedziałku jest obliczana w ten sposób:
Więc jest to w rzeczywistości „iloczyn kropkowy” cen i ilości sprzedanych ciast:
($3, $4, $2) – (13, 8, 6) = $3×13 + $4×8 + $2×6
= $83
Dopasowujemy cenę do tego, ile sprzedano, mnożymy każdą z nich, a następnie sumujemy wynik.
Innymi słowy:
- Sprzedaż w poniedziałek wyniosła: Apple pie: $3×13=$39, Cherry pie: $4×8=$32 i Blueberry pie: $2×6=$12. Razem to jest $39 + $32 + $12 = $83
- A we wtorek: $3×9 + $4×7 + $2×4 = $63
- A w środę: $3×7 + $4×4 + $2×0 = $37
- A w czwartek: $3×15 + $4×6 + $2×3 = $75
Więc ważne jest, aby dopasować każdą cenę do każdej ilości.
Teraz wiesz dlaczego używamy „iloczynu kropkowego”.
A oto pełny wynik w postaci macierzy:

W poniedziałek sprzedali placki warte 83$, we wtorek 63$, itd.
(Możesz wpisać te wartości do kalkulatora macierzowego, aby sprawdzić, czy działają.)
Rows and Columns
Aby pokazać, ile wierszy i kolumn ma macierz, często piszemy rows×columns.
Przykład: Ta macierz ma wymiary 2×3 (2 wiersze na 3 kolumny):
Gdy wykonujemy mnożenie:
- Liczba kolumn pierwszej macierzy musi być równa liczbie wierszy drugiej macierzy.
- A wynik będzie miał taką samą liczbę wierszy jak pierwsza macierz i taką samą liczbę kolumn jak druga macierz.
Przykład:

W tym przykładzie pomnożyliśmy macierz 1×3 przez macierz 3×4 (zauważ, że trójki są takie same), a wynikiem była macierz 1×4.
W ogólności:
Aby pomnożyć macierz m×n przez macierz n×p, n-y muszą być takie same,
a wynikiem jest macierz m×p.
![]()
Więc … mnożąc 1×3 przez 3×1 otrzymujemy wynik 1×1:
Ale mnożąc 3×1 przez 1×3 otrzymujemy wynik 3×3:
Macierz Tożsamości
„Macierz Tożsamości” jest macierzowym odpowiednikiem liczby „1”:
Macierz Tożsamości 3×3
- Jest „kwadratowa” (ma tyle samo wierszy co kolumn)
- Może być duża lub mała (2×2, 100×100, … cokolwiek)
- Ma 1s na głównej przekątnej i 0s wszędzie indziej
- Jej symbolem jest duża litera I
Jest to specjalna macierz, ponieważ kiedy mnożymy przez nią, oryginał pozostaje niezmieniony:
A × I = A
I × A = A
Order mnożenia
W arytmetyce jesteśmy przyzwyczajeni do:
3 × 5 = 5 × 3
(The Commutative Law of Multiplication)
Ale nie jest to na ogół prawdziwe dla macierzy (mnożenie macierzy nie jest komutatywne):
AB ≠ BA
Gdy zmienimy kolejność mnożenia, odpowiedź jest (zazwyczaj) inna.
Przykład:
Zobacz jak zmiana kolejności wpływa na to mnożenie:
Odpowiedzi są różne!
Może mieć ten sam wynik (np. gdy jedna macierz jest macierzą tożsamości), ale nie zwykle.




