Espiras Arquimedeanas são frequentemente usadas na análise de bobinas indutoras, trocadores de calor em espiral e dispositivos microfluídicos. Hoje, vamos demonstrar como construir uma espiral Arquimedeana usando equações analíticas e seus derivados para definir um conjunto de curvas espirais. Com base nestas curvas, vamos então criar uma geometria 2D com espessura específica, extrudando-a para uma geometria 3D completa.
Uma breve introdução às Espirais Arquimedesanas
Largamente observadas na natureza, espirais, ou helices, são utilizadas em muitos projetos de engenharia. Como engenheiro elétrico, por exemplo, você pode enrolar bobinas indutivas em padrões espirais e projetar antenas helicoidais. Como engenheiro mecânico, você pode usar espirais ao projetar molas, engrenagens helicoidais ou mesmo o mecanismo do relógio destacado abaixo.

Um exemplo de uma espiral Arquimedeana usada em um mecanismo de relógio. Imagem de Greubel Forsey. Licenciado por CC BY-SA 3.0, via Wikimedia Commons.
Aqui, vamos focar num tipo específico de espiral, aquela que é apresentada no mecanismo mostrado acima: uma espiral Arquimedeana. Uma espiral Arquimedeana é um tipo de espiral que tem uma distância fixa entre as suas sucessivas voltas. Esta propriedade permite ser amplamente utilizada no desenho de bobinas planas e molas.
Podemos descrever uma espiral Arquimedeana com a seguinte equação em coordenadas polares:
onde a e b são parâmetros que definem o raio inicial da espiral e a distância entre as suas sucessivas voltas, sendo esta última igual a 2 \pi b. Note-se que uma espiral Arquimedeana também é por vezes referida como uma espiral aritmética. Este nome deriva da progressão aritmética da distância da origem ao ponto no mesmo radial.
Desenhando uma Geometria Espiral Parametrizada Arquimedeana
Agora introduzimos as espirais Arquimedeanas, vamos dar uma olhada em como parametrizar e criar tal desenho para análise no COMSOL Multiphysics.
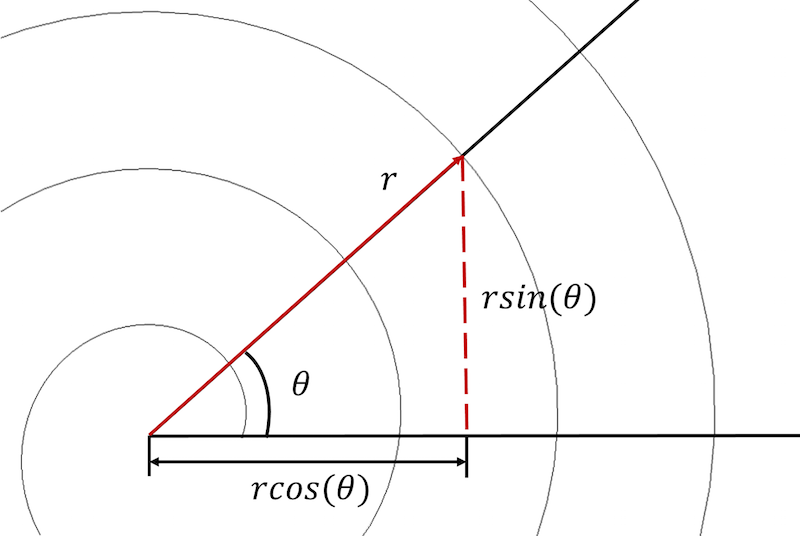
Uma espiral Arquimedeana pode ser descrita tanto em coordenadas polares como cartesianas.
Para começar, precisamos converter as equações espirais de um sistema de coordenadas polares para um sistema de coordenadas cartesianas e expressar cada equação de uma forma paramétrica:
x_{componente}=rcos(\theta)
y_{componente}=rsin(\theta)
{alinhamento*}
Esta transformação permite-nos reescrever a equação da espiral Arquimedesiana de forma paramétrica no sistema de coordenadas cartesianas:
x_{component}=(a+b\theta)cos(\theta) {{component}=(a+b\theta)sin(\theta)
end{align*}
Na COMSOL Multiphysics, é necessário decidir sobre o conjunto de parâmetros que definirão a geometria da espiral. Estes parâmetros são o raio inicial da espiral a_{inicial}, o raio final da espiral a_{final}, e o número desejado de voltas n. A taxa de crescimento da espiral b pode então ser expressa como:
Outras, precisamos decidir sobre o ângulo inicial da espiral theta_0 e o ângulo final theta_f. Comecemos com os valores de theta_0=0 e theta_f=2 \pi n. Com esta informação, podemos definir um conjunto de parâmetros para a geometria da espiral.
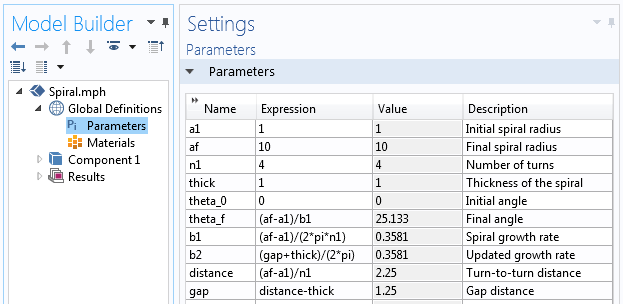
Os parâmetros utilizados para construir a geometria da espiral.
Para construir esta espiral, vamos começar com um Componente 3D e criar um Plano de Trabalho no ramo da Geometria. Na geometria do Plano de Trabalho, adicionamos então uma Curva Paramétrica e usamos as equações paramétricas referenciadas acima com um ângulo variável para desenhar uma versão 2D da espiral Arquimedeana. Estas equações podem ser diretamente inseridas no campo Expressão da curva paramétrica, ou podemos primeiro definir cada equação em uma nova função analítica como:
X_{fun}=(a+bs)cos(s) \\\\
Y_{fun}=(a+bs)sin(s) \\
>end{align*}
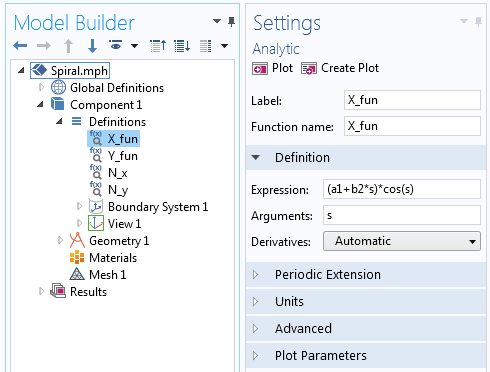
O componente X da equação espiral Arquimedesana definida na função Analítica.
A função Analítica pode ser usada nas expressões para a Curva Paramétrica. Nesta Curva Paramétrica, variamos os parâmetros s do ângulo inicial da espiral, theta_0, até o ângulo final da espiral, theta_f=2 \pi n.
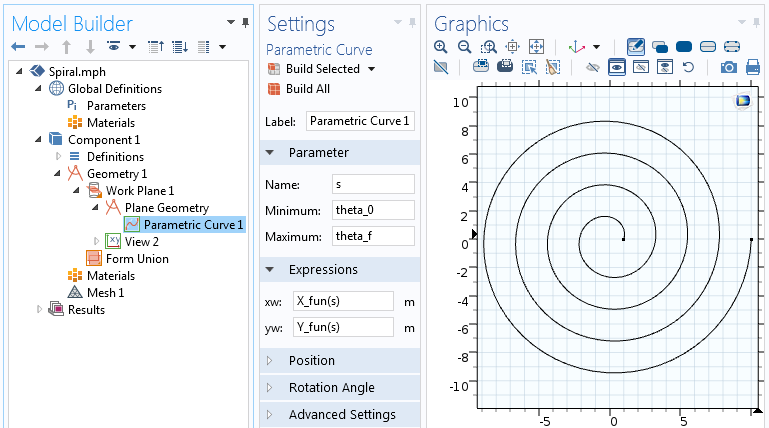
As configurações para o recurso Curva Paramétrica.
As equações paramétricas espirais usadas no recurso Curva Paramétrica resultarão em uma espiral representada por uma curva. Vamos agora construir sobre esta geometria, adicionando-lhe espessura para criar um objecto sólido 2D.
Até agora, a nossa espiral foi parametrizada em termos do raio inicial a_{inicial}, raio final a_{final}, e número desejado de voltas n. Agora, devemos incorporar a espessura como outro parâmetro de controle na equação da espiral.
Vamos começar com a propriedade principal da espiral, que afirma que a distância entre as voltas da espiral é igual a 2 \pi b. Isto também é equivalente a \frac{a_{final}-a_{inicial}}{n}. Para incorporar a espessura, representamos a distância entre cada volta sucessiva da espiral como uma soma da espessura da espiral e do intervalo restante entre as voltas, espessuras+gap.
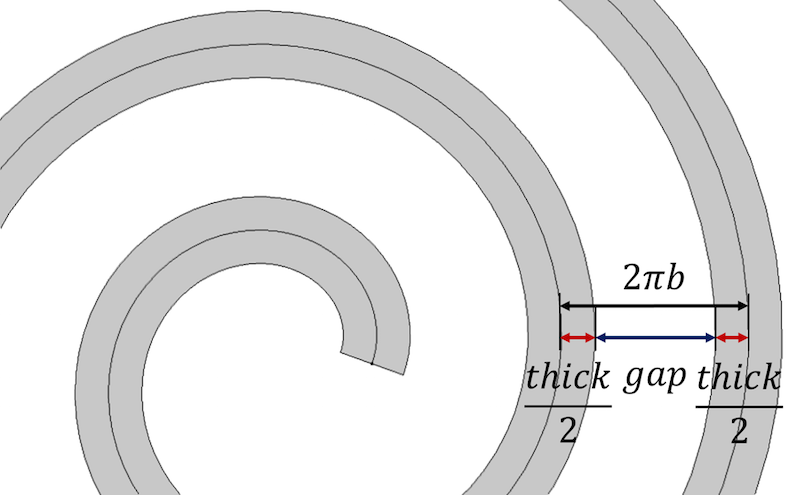
A distância entre as voltas da espiral é definida em termos dos parâmetros de espessura da espiral e intervalo.
Para controlar a espessura e obter uma distância idêntica entre as curvas, a distância pode ser expressa como:
distance=\frac{a_{initial}-a_{final}}{n}
gap=distance-thick
>end{align*}
Após definir a espessura e expressar o intervalo entre as curvas em termos de espessura e distância constante entre as linhas centrais da espiral, podemos reescrever o parâmetro de crescimento da espiral em termos de espessura como:
distance=2\pi b {\31>b=\frac{gap+thick}{2\pi}
>end{alinhamento*}
Também vamos querer expressar o ângulo final da espiral em termos de seus raios inicial e final:
>theta_{final}=2 \pi n \pi n \pi n \pi n \pi n \pi n \pi n \pi n \pi n \pi n \pi n \pi n \pi n \\
a_{final}=2 |pi bn+a_{inicial} \\
n=frac{a_final}-a_{inicial}{2 {pi b}
theta_{final}=frac{2 {2 }pi (a_final}-a_inicial){2 {pi b}
theta_{final}=frac{a_{final}}{b}
end{align*}
Queres iniciar a espiral a partir de um ângulo diferente de zero? Se sim, terá de adicionar este ângulo inicial ao seu ângulo final na expressão do parâmetro: theta_f=\frac{a_{final}-a_{inicial}}{b}+theta_0.
Duplicar duas vezes a curva espiral existente e colocar estas curvas com um desvio de -\frac{thick}{2} e +\frac{thick}{2} em relação à curva espiral inicial permite-nos construir a espiral com espessura. Para posicionar corretamente as espirais superior e inferior, devemos nos certificar de que as espirais de desvio sejam normais em relação à curva espiral inicial. Isto pode ser conseguido multiplicando a distância de desvio \pmfrac{2}{2} pelo vector unitário normal à curva espiral. As equações dos vectores normais para uma curva na forma paramétrica são:
onde s é o parâmetro usado no recurso Curva Paramétrica. Para obter uma unidade normal, precisamos dividir estas expressões pelo comprimento da normal:
As nossas equações paramétricas atualizadas para a espiral Arquimedeana com um deslocamento de meia-escura são:
x_{component}=(a+bs)cos(s)-\frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}\frac{thick}{2} \\y_{component}=(a+bs)sin(s)+frac{dx/ds}{sqrt{(dx/ds)^2+(dy/ds)^2}}}frac{thick}{2}
>end{align*}
Escrever estas equações nos campos de expressão da curva paramétrica pode ser bastante demorado. Como tal, introduzimos a seguinte notação:
N_x=-\frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}} \\
N_y=\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2 }}
\end{align*}
onde cada N_x e N_y é definido através da função Analítica no COMSOL Multiphysics, semelhante a como definimos X_{fun} e Y_{fun} para a primeira curva paramétrica. Dentro da função, utilizamos o operador de diferenciação, d(f(x),x), para tomar a derivada, conforme descrito na seguinte captura de tela.
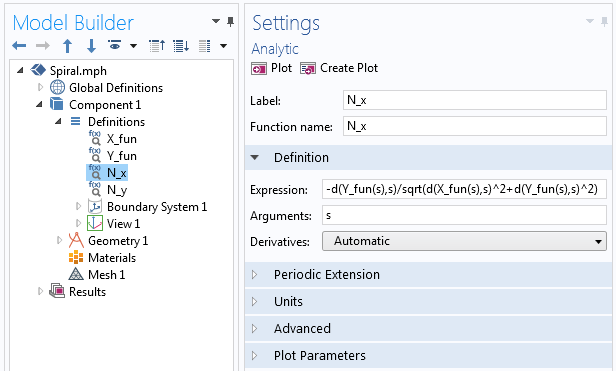
Exemplos do operador derivado utilizado na função Analítica.
As funções X_{fun}, Y_{fun}, N_x, e N_y podem então ser usadas diretamente nas expressões da curva paramétrica para a curva de um lado:
x_{fun}=X_{fun}(s)+N_x(s)\frac{thick}{2} \\
y_{lower}=Y_{fun}(s)+N_y(s)\frac{thick}{2}
\end{align*}
As funções também podem ser usadas para a curva do outro lado:
x_{upper}=X_{fun}(s)-N_x(s)\frac{thick}{2} \\
y_{upper}=Y_{fun}(s)-N_y(s)}frac{thick}{2}
{alinhamento*}
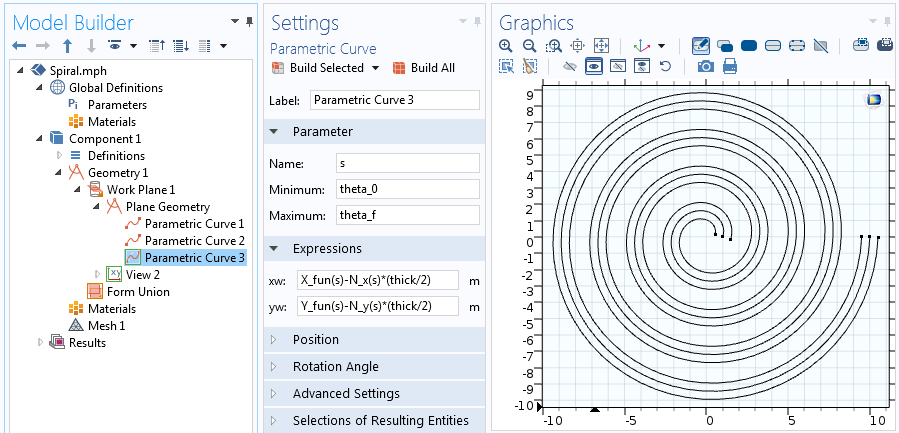
Equações para a segunda das duas curvas paramétricas de offset.
Para juntar as extremidades de duas curvas, adicionamos mais duas curvas paramétricas usando uma ligeira modificação das equações mencionadas acima. Para a curva que une o centro da espiral, temos de avaliar X_{fun}, Y_{fun}, N_x e N_y para o valor inicial do ângulo, theta. Para a curva que une o lado externo da espiral, temos de avaliar o valor final de theta. Portanto, a curva de junção no centro é:
X_{fun}(theta_0)+s\cdot N_x(theta_0)\cdot\frac{thick}{2} \\
Y_{fun}(theta_0)+s\cdot N_y(theta_0)\cdot\frac{thick}{2}
\end{align*}
A curva de junção externa, entretanto, é:
X_{fun}(theta_f)+s\cdot N_x(theta_f){cdot}frac{thick}{2} \\
Y_{fun}(theta_f)+s\cdot N_y(theta_f)\cdot\frac{thick}{2}
\end{align*}
Em ambas as equações acima, s vai de -1 a +1, como mostrado na imagem abaixo.
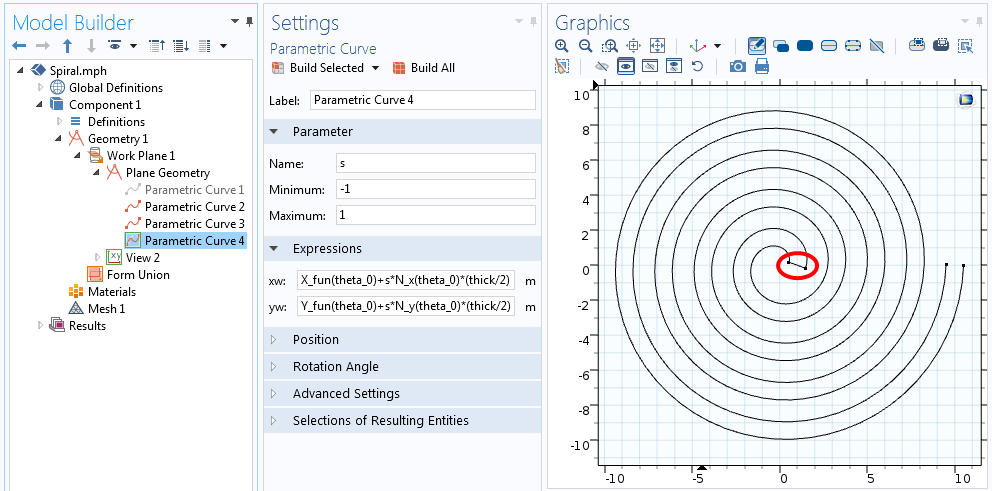
Equações para a curva que une uma extremidade da espiral.
Temos agora cinco curvas que definem a linha de centro da espiral e todos os quatro lados do perfil. Podemos desactivar (ou mesmo apagar) a curva que descreve a linha central, uma vez que não é verdadeiramente necessária, deixando apenas o contorno da espiral. Com o contorno da nossa espiral definido, a operação Converter em Sólido pode ser usada para criar um único objeto geométrico. Esta espiral 2D pode finalmente ser extrudida em 3D através da operação Extrudar.
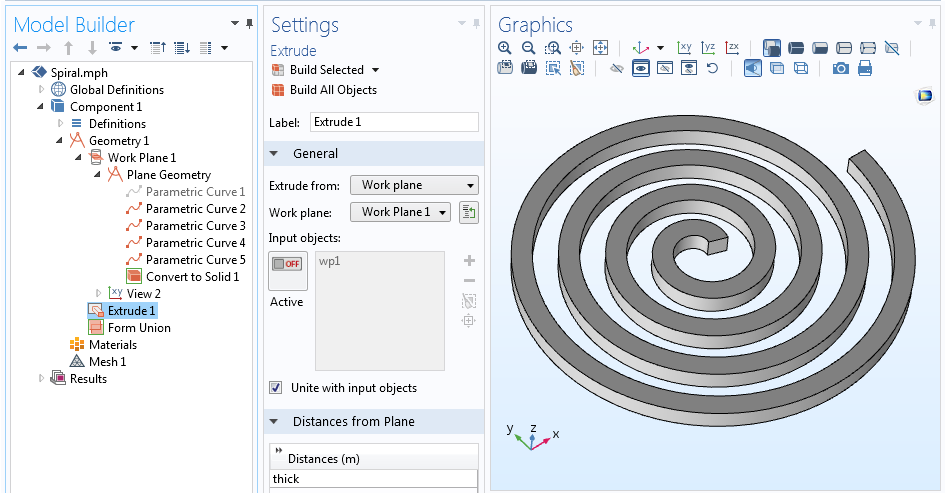
A sequência geométrica completa e a geometria espiral 3D extrudida.
Closing Remarks on Modeling Archimedean Spirals in COMSOL Multiphysics
Passamos os passos para criar uma espiral Archimedean totalmente parametrizada. Com esta geometria em espiral, você pode alterar qualquer um dos parâmetros e experimentar diferentes designs, ou mesmo usá-los como parâmetros em um estudo de otimização. Nós encorajamos você a utilizar esta técnica em seus próprios processos de modelagem, avançando a análise de seu projeto de engenharia particular baseado em espiral.