Arkimedealaisia spiraaleja käytetään usein induktorikelojen, spiraalilämmönvaihtimien ja mikrofluidisten laitteiden analysoinnissa. Tänään näytämme, miten arkimedealainen spiraali rakennetaan käyttämällä analyyttisiä yhtälöitä ja niiden derivaattoja spiraalikäyräjoukon määrittelemiseksi. Näiden käyrien perusteella luomme sitten 2D-geometrian, jolla on tietty paksuus, ja ekstrudoimme sen täydelliseksi 3D-geometriaksi.
Lyhyt johdatus arkimedeeläisiin spiraaleihin
Laajasti luonnossa havaittuja spiraaleja eli kierteitä hyödynnetään monissa teknisissä suunnitelmissa. Sähköinsinöörinä voit esimerkiksi kelata induktiivisia keloja spiraalikuvioihin ja suunnitella spiraaliantenneja. Koneinsinöörinä voit käyttää spiraaleja suunnitellessasi jousia, kierukkavaihteita tai jopa alla esiteltyä kellomekanismia.

Esimerkki arkimedealaisesta spiraalista, jota käytetään kellomekanismissa. Kuva: Greubel Forsey. Lisensoitu CC BY-SA 3.0, Wikimedia Commonsin kautta.
Tässä keskitymme erityiseen spiraalityyppiin, joka on esillä yllä esitetyssä mekanismissa: arkimedeeläiseen spiraaliin. Arkhimedeen spiraali on spiraalityyppi, jonka peräkkäisten kierrosten välillä on kiinteä etäisyys. Tämän ominaisuuden ansiosta sitä käytetään laajalti litteiden kelojen ja jousien suunnittelussa.
Arkimedeuksen spiraalia voidaan kuvata seuraavalla polaarikoordinaatistossa esitetyllä yhtälöllä:
jossa a ja b ovat parametreja, jotka määrittelevät spiraalin alkusäteen ja peräkkäisten kierrosten välisen etäisyyden, joista jälkimmäinen on yhtä suuri kuin 2 \pi b. Huomattakoon, että arkhimedeuslaiseen spiraaliin viitataan toisinaan myös nimellä aritmeettinen spiraali. Tämä nimi juontaa juurensa etäisyyden aritmeettisesta etenemisestä origosta saman radiaalin pisteeseen.
Parametrisoidun arkimedeeläisen spiraaligeometrian suunnittelu
Nyt kun olemme esitelleet arkimedeeläiset spiraalit, katsotaanpa, miten parametrisoida ja luoda tällainen rakenne COMSOL Multiphysicsissä analysoitavaksi.
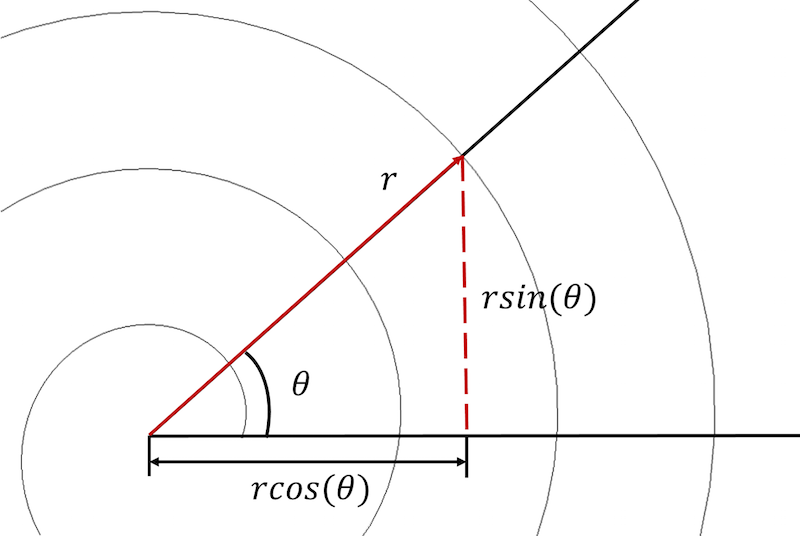
Arkimedeuksen spiraali voidaan kuvata sekä polaari- että kartesiankoordinaatistossa.
Aluksi meidän on muunnettava spiraalin yhtälöt polaarikoordinaatistosta kartesiankoordinaatistoon ja ilmaistava jokainen yhtälö parametrisessa muodossa:
x_{komponentti}=rcos(\theta) \\\
y_{komponentti}=rsin(\theta)
\end{align*}
Tämän muunnoksen avulla voimme kirjoittaa arkimedeeläisen spiraalin yhtälön uudelleen parametrisessa muodossa kartesiankoordinaatistossa:
x_{komponentti}=(a+b\theta)cos(\theta) \\\
y_{komponentti}=(a+b\theta)sin(\theta)
\end{align*}
COMSOL Multiphysics -ohjelmassa on päätettävä parametrien joukko, joka määrittelee spiraalin geometrian. Nämä parametrit ovat spiraalin alkusäde a_initial}, spiraalin loppusäde a_{final} ja haluttu kierrosluku n. Spiraalin kasvunopeus b voidaan tällöin ilmaista seuraavasti:
Seuraavaksi on päätettävä spiraalin aloituskulma theta_0 ja lopetuskulma theta_f. Lähdetään liikkeelle arvoista theta_0=0 ja theta_f=2 \pi n. Näiden tietojen avulla pystymme määrittelemään spiraaligeometrian parametrit.
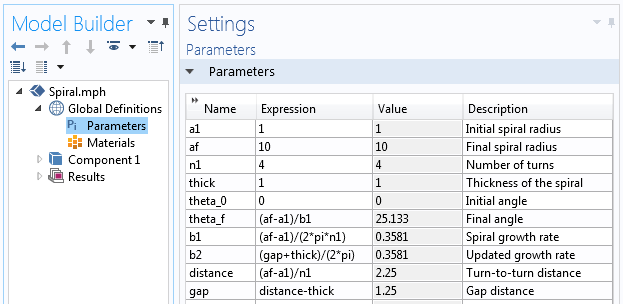
Parametrit, joita käytetään spiraaligeometrian rakentamiseen.
Tämän spiraalin rakentaminen aloitetaan 3D-komponentilla ja luodaan Geometry-haarassa Work Plane. Work Plane -geometriaan lisäämme sitten parametrisen käyrän ja käytämme edellä mainittuja parametrisia yhtälöitä vaihtelevalla kulmalla piirtääksemme 2D-version arkimedealaisesta spiraalista. Nämä yhtälöt voidaan syöttää suoraan parametrisen käyrän Expression-kenttään, tai voimme ensin määritellä jokaisen yhtälön uudessa Analytic-funktiossa seuraavasti:
X_{fun}=(a+bs)cos(s) \\\
Y_{fun}=(a+bs)sin(s) \\\
\end{align*}
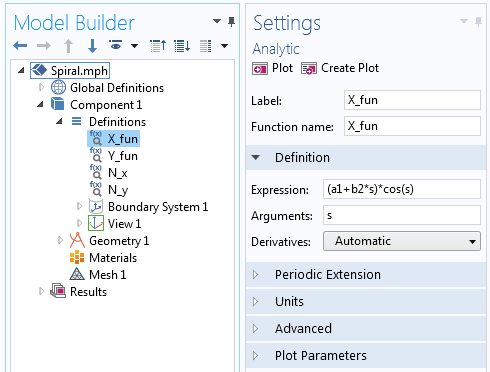
Analyyttisessä funktiossa määritellyn arkimedealaisen spiraalin yhtälön X-komponentti.
Analyyttistä funktiota voidaan käyttää parametrisen käyrän lausekkeissa. Tässä Parametrinen käyrä -funktiossa muuttuu parametri s spiraalin alkukulmasta theta_0 spiraalin loppukulmaan theta_f=2 \pi n.
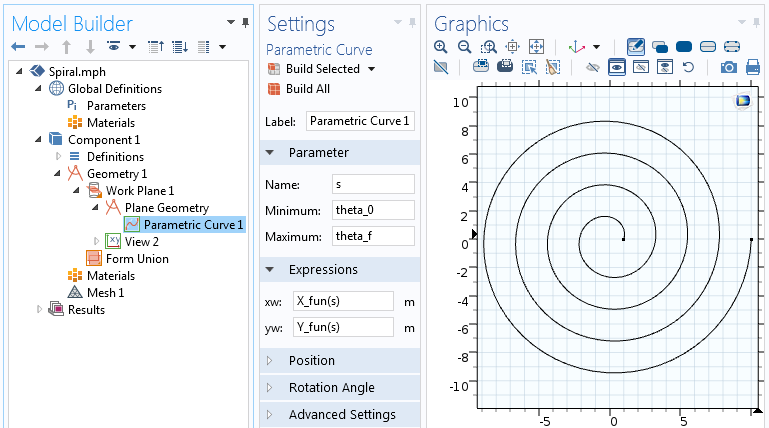
Parametrinen käyrä -toiminnon asetukset.
Parametrinen käyrä -toiminnossa käytetyt parametriset spiraaliyhtälöt johtavat spiraalin esittämiseen käyränä. Rakennetaan nyt tämän geometrian päälle lisäämällä siihen paksuutta, jotta saadaan luotua 2D-solidi objekti.
Tähän asti spiraalimme on parametrisoitu alkusäteen a_{initial}, loppusäteen a_{final} ja halutun kierrosluvun n suhteen. Nyt meidän on sisällytettävä paksuus toisena säätöparametrina spiraalin yhtälöön.
Aloitetaan spiraalin pääominaisuudesta, jonka mukaan spiraalin kierrosten välinen etäisyys on yhtä suuri kuin 2 \pi b. Tämä vastaa myös \frac{a_{final}-a_{initial}}{n}. Paksuuden huomioon ottamiseksi esitämme spiraalin jokaisen peräkkäisen kierroksen välisen etäisyyden spiraalin paksuuden ja kierrosten väliin jäävän raon summana, thick+gap.
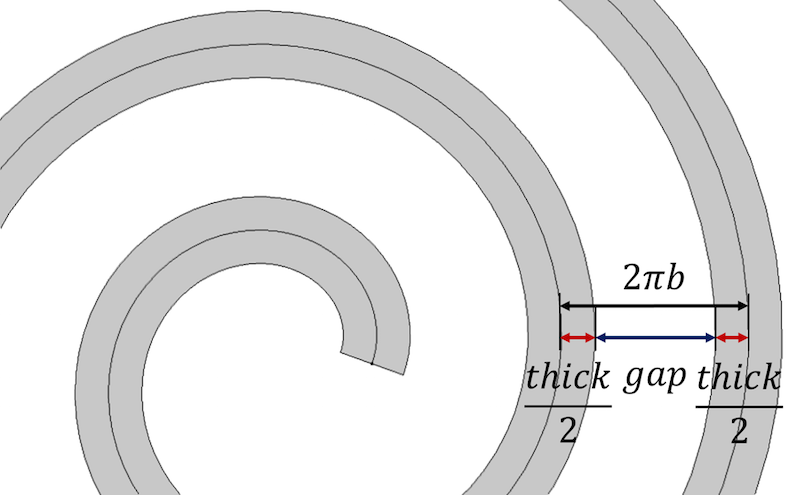
Spiraalin kierrosten välinen etäisyys määritellään spiraalin paksuus- ja rakoparametrien avulla.
Paksuuden hallitsemiseksi ja identtisen etäisyyden saamiseksi kierrosten välille etäisyys voidaan ilmaista seuraavasti:
distance=\frac{a_{initial}-a_{final}}}{n} \\\
gap=distance-thick
\end{align*}
Määriteltyämme paksuuden ja ilmaistuamme kierrosten välisen kuilun paksuuden ja spiraalin keskilinjojen vakioetäisyyden avulla, voimme kirjoittaa spiraalin kasvuparametrin uudelleen paksuuden avulla seuraavasti:
distance=2\pi b \\\
b=\frac{gap+thick}{2\pi}
\end{align*}
Haluamme myös ilmaista spiraalin lopullisen kulman sen alku- ja loppusäteiden suhteen:
\theta_{final}=2 \pi n \\\
a_{final}=\text{kokonaisetäisyys}+a_{initial} \\\
a_{final}=2 \pi bn+a_{initial} \\\
n=\frac{a_{final}-a_{initial}}{2 \pi b} \\\
\theta_{final}=\frac{2 \pi (a_{final}-a_{initial})}{2 \pi b} \\
\theta_{final}=\frac{a_{final}-a_{initial}}{b}{b}
\end{align*}
Haluatko aloittaa spiraalin muusta kuin nollakulmasta? Jos näin on, sinun on lisättävä tämä alkukulma loppukulmaan parametrin lausekkeessa: theta_f=\frac{a_{final}-a_{initial}}{b}+theta_0.
Kaksinkertaistamalla olemassa oleva spiraalikäyrä kahdesti ja sijoittamalla nämä käyrät -\frac{paksumman}{2} ja +\frac{paksumman}{2} -siirtymällä alkuperäisen spiraalikäyrän suhteen voimme rakentaa spiraalin paksumman. Jotta ylempi ja alempi spiraali voidaan sijoittaa oikein, on varmistettava, että offset-spiraalit ovat normaaleja alkuperäiseen spiraalikäyrään nähden. Tämä voidaan saavuttaa kertomalla offset-etäisyys \pm\frac{thick}{2} spiraalikäyrään nähden normaalilla yksikkövektorilla. Käyrän normaalivektoreiden yhtälöt parametrimuodossa ovat:
jossa s on parametri, jota käytetään parametrisen käyrän ominaisuudessa. Saadaksemme yksikkönormaalin, meidän on jaettava nämä lausekkeet normaalin pituudella:
Päivitetyt parametriset yhtälömme arkimedealaiselle spiraalille, jossa on puolen paksuuden siirtymä, ovat:
x_{component}=(a+bs)cos(s)-\frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}\frac{thick}{2} \\
y_{komponentti}=(a+bs)sin(s)+\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}\frac{thick}{2}
\end{align*}
Tämän yhtälön kirjoittaminen parametrikäyrän lausekekenttiin voi olla melko aikaa vievää. Siksi otamme käyttöön seuraavan merkintätavan:
N_x=-\frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}} \\
N_y=\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2 }}
\end{align*}
jossa kukin N_x ja N_y määritellään COMSOL Multiphysicsin Analytic-funktion avulla samalla tavalla kuin määrittelimme X_{fun} ja Y_{fun} ensimmäiselle parametrikäyrälle. Funktion sisällä käytämme differentiointioperaattoria, d(f(x),x), derivaatan ottamiseen, kuten seuraavassa kuvakaappauksessa on esitetty.
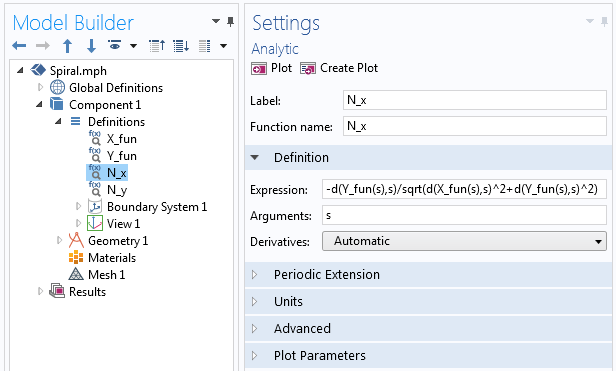
Esimerkkejä Analytic-funktiossa käytetystä derivaattaoperaattorista.
Funktioita X_{fun}, Y_{fun}, N_x ja N_y voidaan tällöin käyttää suoraan parametrikäyrän lausekkeissa toisella puolella olevan käyrän osalta:
x_{lower}=X_{fun}(s)+N_x(s)\frac{thick}{2} \\
y_{lower}=Y_{fun}(s)+N_y(s)\frac{thick}{2}
\end{align*}
Funktioita voidaan käyttää myös toisella puolella olevalle käyrälle:
x_{upper}=X_{fun}(s)-N_x(s)\frac{thick}{2} \\
y_{upper}=Y_{fun}(s)-N_y(s)\frac{thick}{2}
\end{align*}
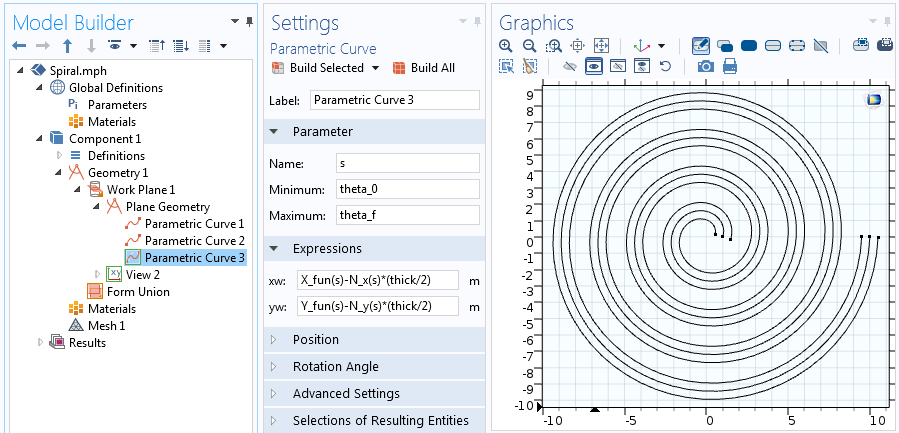
Yhtälöt toiselle kahdesta offset-parametrikäyrästä.
Kahden käyrän päiden liittämiseksi toisiinsa lisäämme vielä kaksi parametrikäyrää käyttäen pientä muunnosta edellä mainituista yhtälöistä. Käyrälle, joka yhdistää spiraalin keskipisteen, meidän on arvioitava X_{fun}, Y_{fun}, N_x ja N_y kulman alkuarvolle, theta. Käyrälle, joka liittyy spiraalin ulkoreunaan, on arvioitava thetan loppuarvo. Liittyvä käyrä keskellä on siis:
X_{fun}(theta_0)+s\cdot N_x(theta_0)\cdot\frac{thick}{2} \\
Y_{fun}(theta_0)+s\cdot N_y(theta_0)\cdot\frac{thick}{2}
\end{align*}
Ulkoinen liitoskäyrä on puolestaan:
X_{fun}(theta_f)+s\cdot N_x(theta_f)\cdot\frac{thick}{2} \\
Y_{fun}(theta_f)+s\cdot N_y(theta_f)\cdot\frac{thick}{2}
\end{align*}
Kummassakin ylläolevassa yhtälössä s menee -1:stä +1:een, kuten alla olevassa kuvakaappauksessa näkyy.
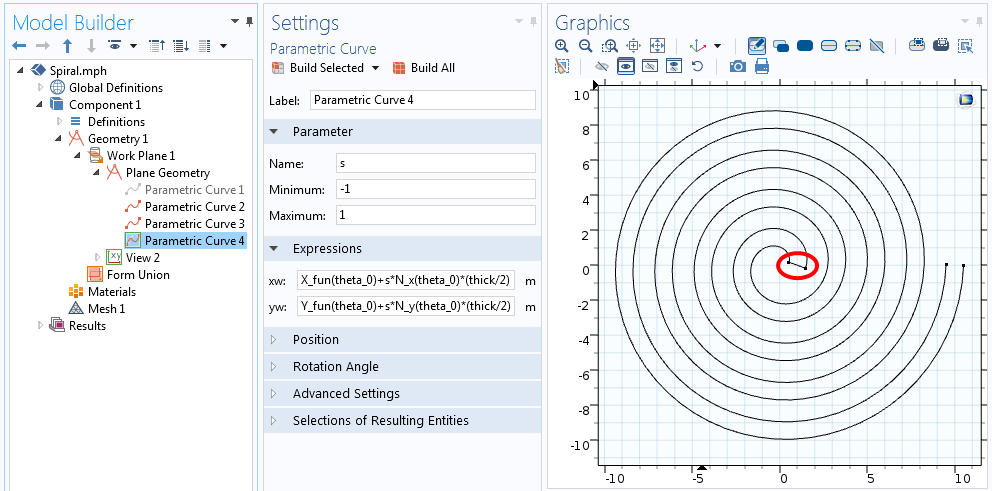
Yhtälöt käyrälle, joka yhdistää spiraalin toisen pään.
Meillä on nyt viisi käyrää, jotka määrittelevät spiraalin keskilinjan ja profiilin kaikki neljä sivua. Voimme poistaa (tai jopa poistaa) keskilinjaa kuvaavan käyrän käytöstä, koska se ei ole todella tarpeellinen, jolloin jäljelle jää vain spiraalin ääriviivat. Kun spiraalin ääriviivat on määritelty, Convert to Solid -operaatiolla voidaan luoda yksi geometriaobjekti. Tämä 2D-spiraali voidaan lopuksi ekstrudoida 3D:ksi Extrude-operaatiolla.
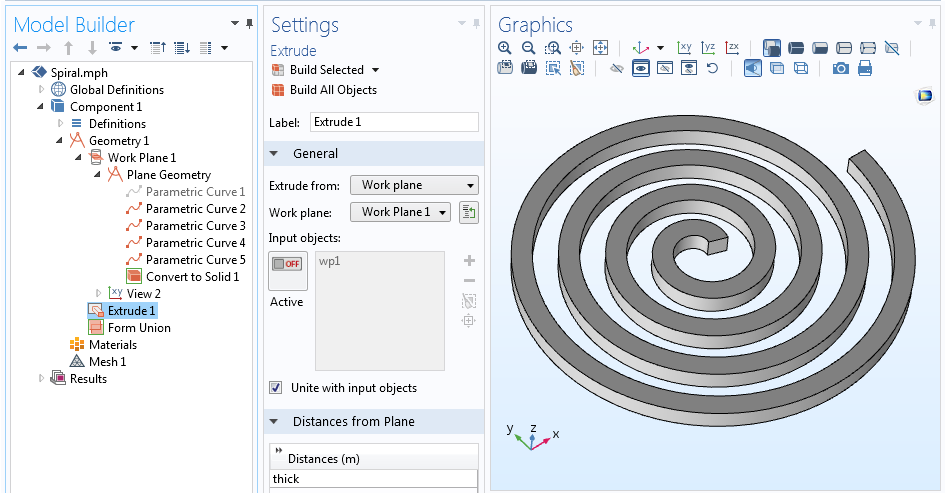
Kokonaisgeometriasekvenssi ja ekstrudoitu 3D-spiraaligeometria.
Loppuhuomautuksia arkimedealaisten spiraalien mallintamisesta COMSOL Multiphysicsissä
Olemme käyneet läpi vaiheet, joiden avulla luomme täysin parametrisoidun arkimedealaisen spiraalin. Tämän spiraaligeometrian avulla voit muuttaa mitä tahansa parametreja ja kokeilla erilaisia malleja tai jopa käyttää niitä parametreina optimointitutkimuksessa. Kannustamme sinua hyödyntämään tätä tekniikkaa omissa mallinnusprosesseissasi ja edistämään tietyn spiraalipohjaisen teknisen suunnittelun analyysia.