Az archimédeszi spirálokat gyakran használják induktor tekercsek, spirális hőcserélők és mikrofluidikai eszközök elemzésére. Ma bemutatjuk, hogyan építhetünk fel egy archimédeszi spirált analitikus egyenletek és azok deriváltjainak segítségével, hogy meghatározzuk a spirálgörbék egy halmazát. Ezekre a görbékre alapozva ezután létrehozunk egy 2D-s geometriát meghatározott vastagsággal, majd extrudáljuk azt egy teljes 3D-s geometriává.
A rövid bevezetés az archimédeszi spirálokba
A természetben széles körben megfigyelhető spirálokat, vagy spirálokat számos mérnöki konstrukcióban hasznosítják. Villamosmérnökként például induktív tekercseket tekercselhetünk spirális mintázatokba, és spirális antennákat tervezhetünk. Gépészmérnökként spirálokat használhatsz rugók, spirális fogaskerekek vagy akár az alább kiemelt óraművek tervezésénél.

Egy óraműben használt archimédeszi spirál példája. A képet a Greubel Forsey készítette. Licensed by CC BY-SA 3.0, via Wikimedia Commons.
Itt most a spirál egy speciális típusára összpontosítunk, arra, amely a fent látható mechanizmusban szerepel: az archimédeszi spirálra. Az archimédeszi spirál olyan spiráltípus, amelynek egymást követő fordulatai között rögzített távolság van. Ez a tulajdonsága lehetővé teszi, hogy széles körben használják lapos tekercsek és rugók tervezésénél.
Az archimédeszi spirált a következő egyenlet segítségével írhatjuk le polárkoordinátákban:
ahol a és b a spirál kezdeti sugarát és az egymást követő fordulatok közötti távolságot meghatározó paraméterek, amelyek közül az utóbbi egyenlő 2 \pi b-vel. Megjegyezzük, hogy az archimédeszi spirált néha aritmetikai spirálnak is nevezik. Ez az elnevezés az origótól az azonos radiálon lévő pontok távolságának számtani haladásától származik.
Paraméterezett archimédeszi spirálgeometria tervezése
Most, hogy bemutattuk az archimédeszi spirálokat, nézzük meg, hogyan lehet egy ilyen tervet paraméterezni és létrehozni a COMSOL Multiphysics-ben történő elemzéshez.
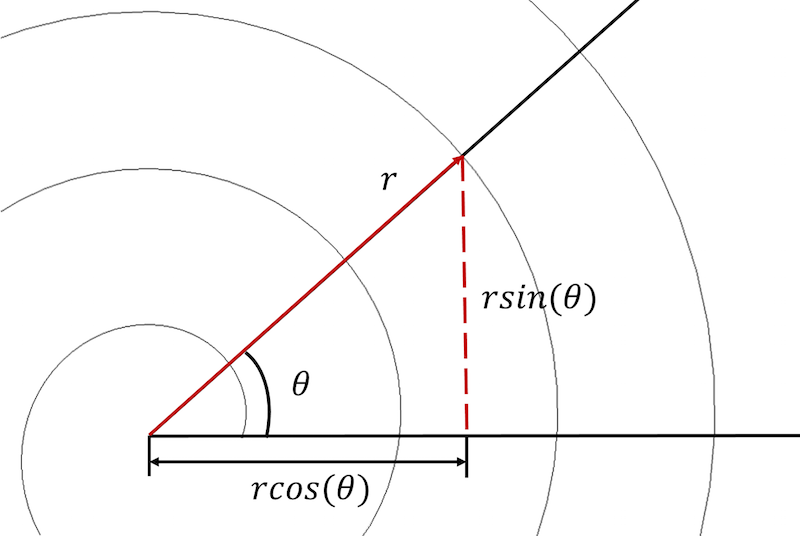
Egy archimédeszi spirál poláris és kartéziánus koordinátákban is leírható.
Kezdésként a spirál egyenleteit poláris koordinátarendszerből kartéziánus koordinátarendszerbe kell konvertálnunk, és minden egyenletet paraméteres formában kell kifejeznünk:
x_{komponens}=rcos(\theta) \\\
y_{komponens}=rsin(\theta)
\end{align*}
Ez az átalakítás lehetővé teszi, hogy az archimédeszi spirál egyenletét paraméteres formában átírjuk a kartéziánus koordinátarendszerben:
x_{komponens}=(a+b\theta)cos(\theta) \\\
y_{komponens}=(a+b\theta)sin(\theta)
\end{align*}
A COMSOL Multiphysics-ben el kell dönteni, hogy a spirál geometriáját milyen paraméterek fogják meghatározni. Ezek a paraméterek a spirál kezdeti sugara a_{initial}, a spirál végső sugara a_{final}, és a kívánt fordulatszám n. A spirál növekedési sebessége b ezután a következőképpen fejezhető ki:
A továbbiakban döntenünk kell a spirál kezdőszögéről theta_0 és végszögéről theta_f. Kezdjük a theta_0=0 és theta_f=2 \pi n értékekkel. Ezekkel az információkkal képesek vagyunk meghatározni a spirálgeometria paraméterkészletét.
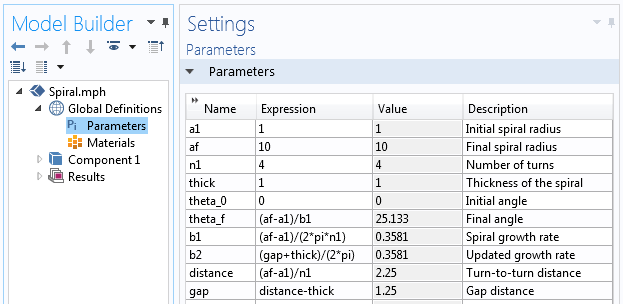
A spirálgeometria felépítéséhez használt paraméterek.
A spirál felépítéséhez egy 3D komponenssel kezdünk, és létrehozunk egy munkasíkot a Geometria ágban. A Munkasík geometriában ezután hozzáadunk egy Parametrikus görbét, és a fent hivatkozott paraméteres egyenleteket használjuk változó szöggel az archimédeszi spirál 2D-s változatának megrajzolásához. Ezeket az egyenleteket közvetlenül beírhatjuk a parametrikus görbe Kifejezés mezőjébe, vagy először minden egyenletet definiálhatunk egy új Analitikus függvényben a következőképpen:
X_{fun}=(a+bs)cos(s) \\\
Y_{fun}=(a+bs)sin(s) \\\
\end{align*}
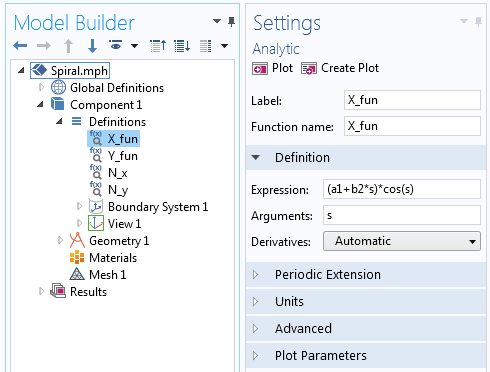
Az Analytic függvényben definiált archimédeszi spirál egyenlet X-komponense.
Az Analitikus függvény használható a Parametrikus görbére vonatkozó kifejezésekben. Ebben a Parametrikus görbében az s paramétert a spirál kezdeti szögétől, theta_0-tól a spirál végső szögéig, theta_f=2 \pi n.
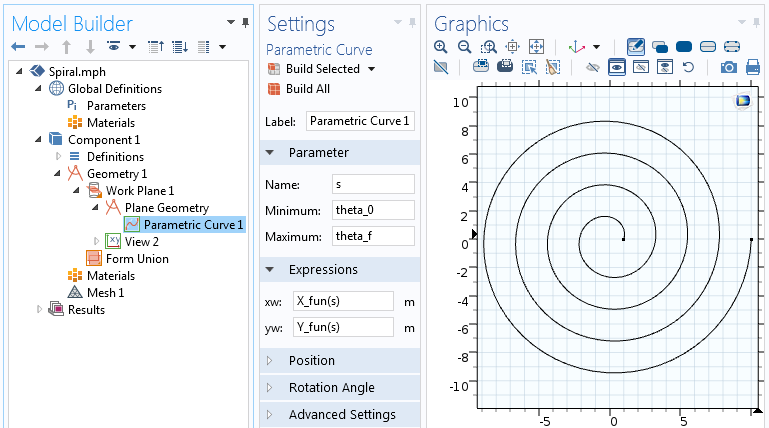
A Parametrikus görbe funkció beállításai.
A Parametrikus görbe funkcióban használt parametrikus spirál egyenletek egy görbe által ábrázolt spirált eredményeznek. Most építsünk erre a geometriára, vastagságot adva hozzá, hogy egy 2D-s szilárd objektumot hozzunk létre.
Edig a pontig a spirálunkat az a_{initial} kezdeti sugárral, az a_{final} végső sugárral és a kívánt n fordulatszámmal paramétereztük. Most a spirál egyenletébe be kell építenünk a vastagságot, mint egy másik vezérlő paramétert.
Kezdjük a spirál fő tulajdonságával, amely szerint a spirálfordulók közötti távolság egyenlő 2 \pi b-vel. Ez megegyezik \frac{a_{végleges}-a_{kezdeti}-a_{kezdeti}}{n} értékkel is. A vastagság beépítéséhez a spirál egyes egymást követő fordulatai közötti távolságot a spirál vastagságának és a fordulók között fennmaradó résnek az összegeként, vastag+résként ábrázoljuk.
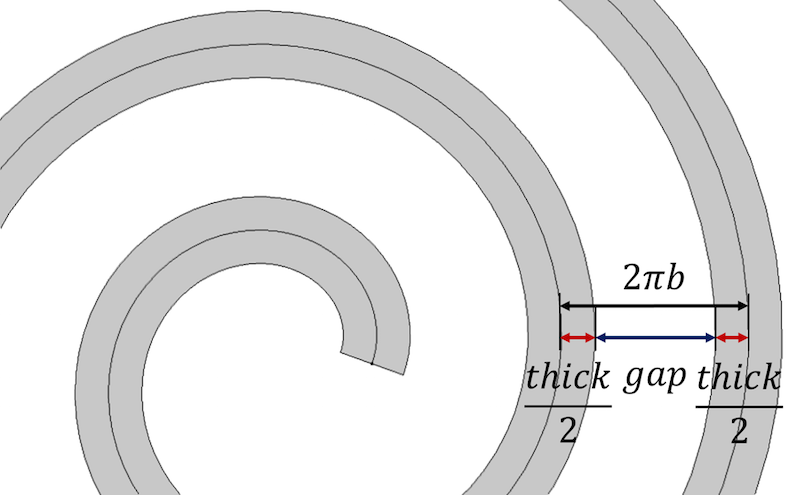
A spirálfordulók közötti távolságot a spirál vastagság és a rés paramétereivel határozzuk meg.
A vastagság szabályozásához és a fordulók közötti azonos távolság eléréséhez a távolság a következőképpen fejezhető ki:
distance=\frac{a_{initial}-a_{final}}}{n}{n} \\\
hézag=távolságvastagság
\vég{align*}
A vastagság meghatározása és a fordulók közötti hézag vastagsággal és a spirál középvonalai közötti állandó távolsággal való kifejezése után a spirál növekedési paraméterét a vastagsággal kifejezve a következőképpen írhatjuk át:
distance=2\pi b \\\
b=\frac{hézag+vastagság}{2\pi}
\end{align*}
A spirál végső szögét is ki akarjuk fejezni a kezdeti és végső sugarakkal:
\theta_{final}=2 \pi n \\\
a_{final}=\text{teljes távolság}+a_{initial} \\\
a_{végleges}=2 \pi bn+a_{kezdeti} \\\
n=\frac{a_{végső}-a_{kezdeti}}}{2 \pi b} \\\
\theta_{végső}=\frac{2 \pi (a_{végső}-a_{kezdeti})}{2 \pi b} \\\
\theta_{végső}=\frac{a_{végső}-a_{kezdeti}}{b}
\end{align*}
A spirált a nullától eltérő szögből akarjuk indítani? Ha igen, akkor ezt a kezdeti szöget hozzá kell adni a végső szöghez a paraméterre vonatkozó kifejezésben: theta_f=\frac{a_{végső}-a_{kezdeti}}{b}+theta_0.
A meglévő spirálgörbét kétszer megduplázva és ezeket a görbéket a kezdeti spirálgörbéhez képest -\frac{vastag}{2} és +\frac{vastag}{2} eltolással elhelyezve tudjuk a spirált vastagsággal felépíteni. A felső és alsó spirálok helyes elhelyezéséhez meg kell győződnünk arról, hogy az eltolt spirálok merőlegesek a kezdeti spirálgörbére. Ezt úgy érhetjük el, hogy az eltolási távolságot \pm\frac{thick}{2} megszorozzuk a spirálgörbére merőleges egységvektorral. A görbére vonatkozó normálvektorok egyenletei paraméteres formában a következők:
ahol s a Parametrikus görbe tulajdonságban használt paraméter. Ahhoz, hogy egységnormált kapjunk, ezeket a kifejezéseket el kell osztanunk a normális hosszával:
Az archimédeszi spirálra vonatkozó frissített paraméteres egyenleteink fél vastagság eltolással a következők:
x_{component}=(a+bs)cos(s)-\frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}\frac{thick}{2} \\
y_{komponens}=(a+bs)sin(s)+\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}\frac{thick}{2}
\end{align*}
Az egyenletek kiírása a parametrikus görbe kifejezésmezőiben meglehetősen időigényes lehet. Ezért a következő jelölést vezetjük be:
N_x=-\frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}} \\
N_y=\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2 }}
\end{align*}
ahol minden N_x és N_y a COMSOL Multiphysics analitikus függvényén keresztül van definiálva, hasonlóan ahhoz, ahogyan az első parametrikus görbe esetében az X_{fun} és Y_{fun} értékeket definiáltuk. A függvényen belül a d(f(x),x) differenciálási operátort használjuk a deriváláshoz, ahogy az a következő képernyőképen látható.
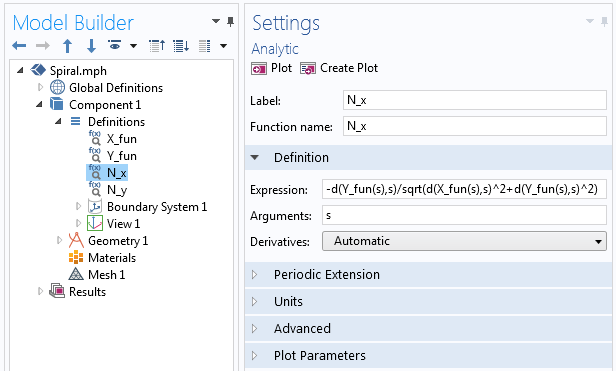
Példák az Analytic függvényben használt deriválási operátorra.
Az X_{fun}, Y_{fun}, N_x és N_y függvények ezután közvetlenül felhasználhatók a parametrikus görbe egyik oldalán lévő görbe kifejezéseiben:
x_{lower}=X_{fun}(s)+N_x(s)\frac{thick}{2} \\
y_{lower}=Y_{fun}(s)+N_y(s)\frac{thick}{2}
\end{align*}
A függvények a másik oldalon lévő görbére is használhatók:
x_{upper}=X_{fun}(s)-N_x(s)\frac{thick}{2} \\
y_{upper}=Y_{fun}(s)-N_y(s)\frac{thick}{2}
\end{align*}
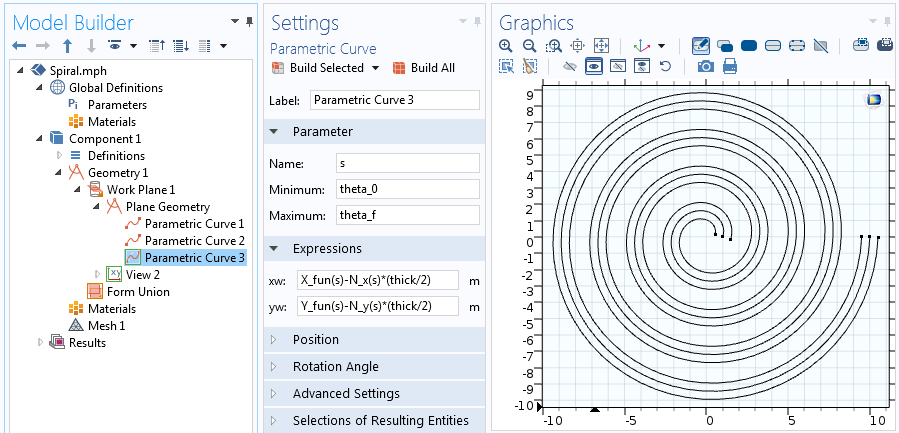
Egyenletek a két eltolt parametrikus görbe közül a másodikra.
A két görbe végeinek összekötéséhez a fent említett egyenletek kismértékű módosításával még két parametrikus görbét adunk hozzá. A spirál középpontját összekötő görbéhez ki kell értékelnünk X_{fun}, Y_{fun}, N_x és N_y értékeket a szög kezdőértékére, theta-ra. A spirál külső oldalához csatlakozó görbe esetében a theta végső értékét kell kiértékelnünk. Ezért a középen csatlakozó görbe:
X_{fun}(theta_0)+s\cdot N_x(theta_0)\cdot\frac{thick}{2} \\
Y_{fun}(theta_0)+s\cdot N_y(theta_0)\cdot\frac{thick}{2}
\end{align*}
A külső csatlakozási görbe eközben:
X_{fun}(theta_f)+s\cdot N_x(theta_f)\cdot\frac{thick}{2} \\
Y_{fun}(theta_f)+s\cdot N_y(theta_f)\cdot\frac{thick}{2}
\end{align*}
A fenti két egyenletben s -1-ről +1-re megy, ahogy az alábbi képernyőképen látható.
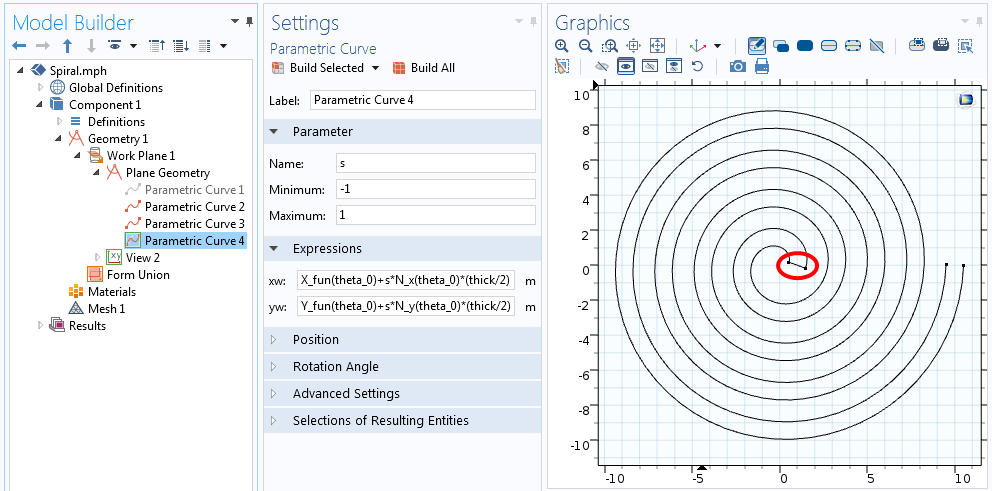
A spirál egyik végét összekötő görbére vonatkozó egyenletek.
Most öt görbénk van, amelyek meghatározzák a spirál középvonalát és a profil mind a négy oldalát. A középvonalat leíró görbét kikapcsolhatjuk (vagy akár törölhetjük is), mivel nem igazán szükséges, így csak a spirál körvonala marad. A spirál körvonalának meghatározásával a Convert to Solid művelet segítségével egyetlen geometriai objektumot hozhatunk létre. Ez a 2D-s spirál végül az Extrude művelettel 3D-be extrudálható.
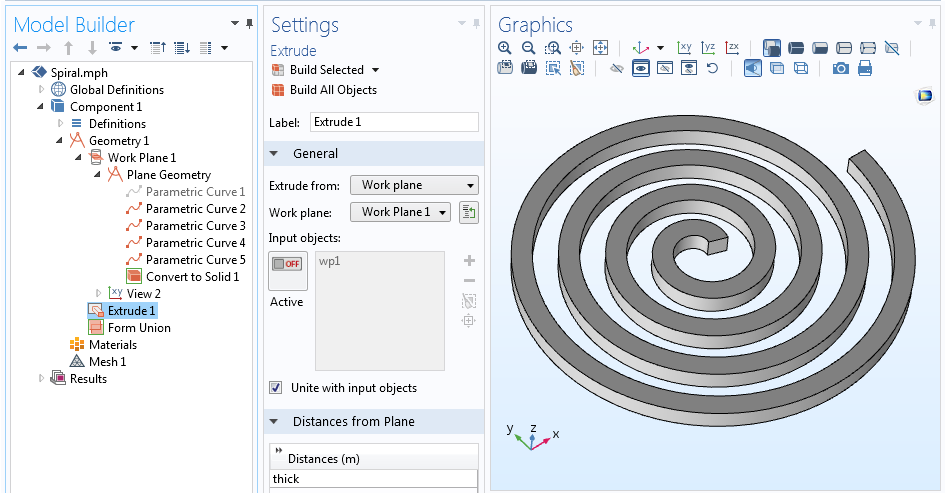
A teljes geometriasorozat és az extrudált 3D-s spirálgeometria.
Záró megjegyzések az archimédeszi spirálok modellezéséhez a COMSOL Multiphysicsben
Megmutattuk a teljesen paraméterezett archimédeszi spirál létrehozásának lépéseit. Ezzel a spirálgeometriával bármelyik paramétert megváltoztathatja, és különböző konstrukciókkal kísérletezhet, vagy akár paraméterként is használhatja őket egy optimalizációs vizsgálatban. Arra bátorítjuk, hogy használja ezt a technikát saját modellezési folyamataiban, előmozdítva ezzel az adott spirál alapú mérnöki tervezés elemzését.