アルキメデス螺旋は、インダクタコイル、螺旋状熱交換器、マイクロ流体装置の解析でよく使用されています。 本日は、解析方程式とその導関数を用いてアルキメデス螺旋を構築し、螺旋曲線のセットを定義する方法を紹介します。 これらの曲線に基づいて、特定の厚みを持つ 2D ジオメトリを作成し、それを完全な 3D ジオメトリに押し出します。
A Brief Introduction to Archimedean Spirals
自然界で広く観察される螺旋またはヘリは、多くの工学設計に利用されます。 たとえば、電気技術者であれば、誘導コイルを螺旋状に巻いたり、ヘリカルアンテナを設計したりすることができます。 機械技師として、ばね、らせん歯車、または以下に示す時計のメカニズムを設計するときに、らせんを使用することができます。 画像:Greubel Forsey。 Licensed by CC BY-SA 3.0, via Wikimedia Commons.
ここでは、上に示した機構に使われている、ある特定の種類の螺旋、つまりアルキメデス螺旋に焦点を当てます。 アルキメデス螺旋とは、螺旋の一種で、連続した回転の間隔が一定であるものである。
アルキメデス螺旋は極座標で次の式で表される。
ここでa、bは螺旋の初期半径と連続回転間の距離で、後者は2 \pi bに等しいパラメータである。 この名前は、原点から同じ半径上の点までの距離が算術的に進むことに由来します。
パラメータ化されたアルキメデス螺旋形状の設計
アルキメデス螺旋についてご紹介しましたが、次にCOMSOL Multiphysicsで解析するためのパラメータ化と作成方法を見てみましょう。
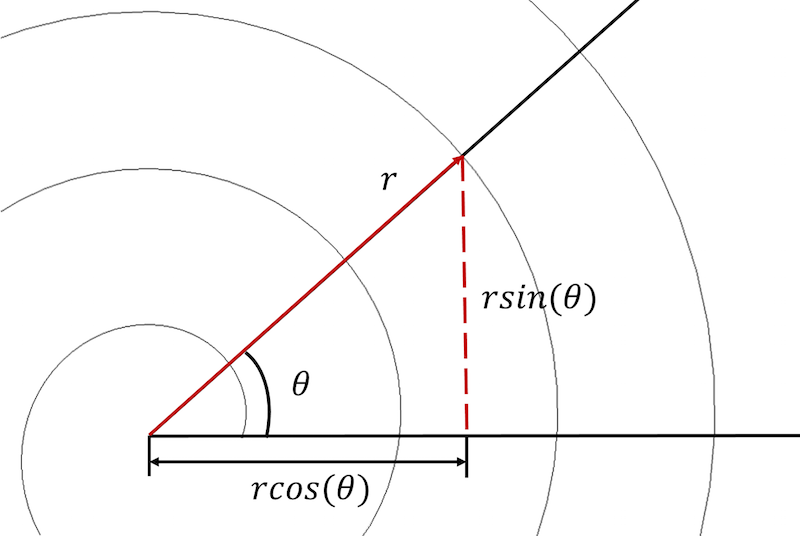
アルキメデス螺旋は、極座標とデカルト座標の両方で記述できます。
まず、螺旋方程式を極座標系からデカルト系に変換し、各式をパラメトリック形式で表現することが必要です。
x_{component}=rcos(\theta) \
y_{component}=rsin(\theta)
\end{align*}
この変換によりアルキメデス螺旋の方程式をパラメトリック形式でデカルト系で書き直せば良いことになります。
x_{component}=(a+btheta)cos(\theta) \
y_{component}=(a+btheta)sin(\theta)
↩end{align*}
COMSOL Multiphysicsにおいて、螺旋形状を決定するパラメータ群を決定しておく必要がある。 スパイラルの初期半径a_{initial}、最終半径a_{final}、回転数nがパラメータとなり、スパイラルの成長率bは次のように表されます。 この情報により、螺旋形状のパラメータを定義できます。
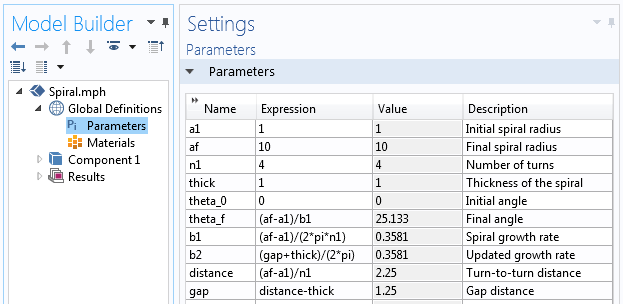
The parameters used to build the spiral geometry.
この螺旋を構築するには、まず 3D Component を作成して Geometry ブランチに Work Plane を作成します。 Work Plane ジオメトリにパラメトリック カーブを追加し、角度を変えながら上記のパラメトリック方程式を使用して、アルキメデス螺旋の 2D バージョンを描画します。 これらの方程式はパラメトリック曲線のExpressionフィールドに直接入力することもできますが、まず新しいAnalytic関数で各方程式を次のように定義します。
X_{fun}=(a+bs)cos(s) \
Y_{fun}=(a+bs)sin(s) \
end{align*}
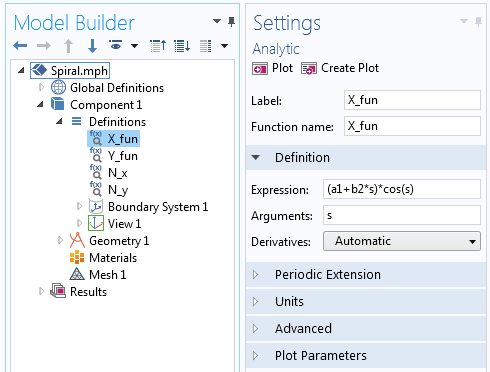
The X-component of the Archimedean spiral equation defined in the Analytic function.
Analytic関数はParametric Curveの式に使うことができる。 このParametric Curveでは、スパイラルの初期角度θ_0からスパイラルの最終角度θ_f=2 \pi nまでパラメータsを変化させます。
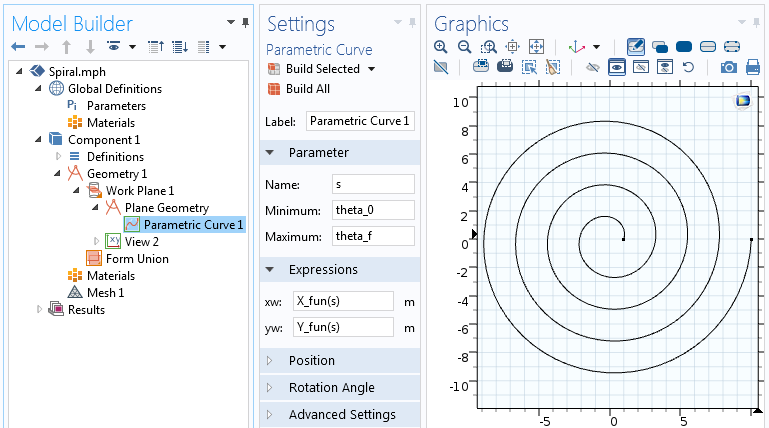
Parametric Curve機能の設定
Parametric Curve機能で用いるパラメトリックスパイラル方程式は、曲線で表されるスパイラルとなる。
ここまでで、スパイラルは初期半径 a_{initial}、最終半径 a_{final}、希望する回転数 n をパラメータ化しました。
まず、スパイラルの主な性質として、スパイラルのターン間の距離は2 \pi bに等しいということがあります。 厚さを組み込むために、スパイラルの連続する各ターン間の距離をスパイラルの厚さとターン間の残りのギャップ、thick+gapの合計として表す。
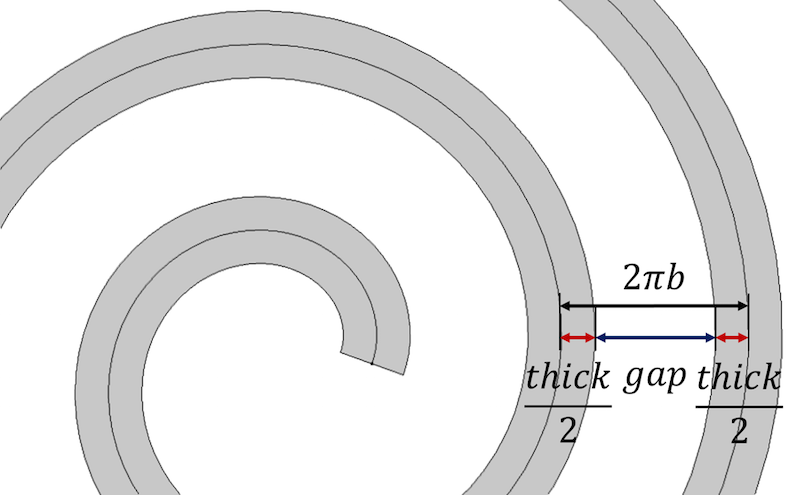
スパイラルのターン間の距離はスパイラルの厚さとギャップパラメータで定義されている。
厚さを制御し、ターン間の距離を同一にするために、距離は次のように表すことができます:
gap=distance-thick
therapeutic end{align*}
厚さを定義し、ターン間のギャップを厚さとスパイラルの中心線間の一定距離で表現すると、スパイラルの成長パラメータを厚さで書き直すと、次のようになる。
distance=2\pi b \
b=themphrac{gap+thick}{2pi}
theend{align*}
またスパイラルの最終角度を初期半径と最終半径で表現したいと思う。
theta_{final}=2 \pi n \
a_{final}=text{total distance}+a_{initial} \p bn+a_{initial}=2 \
n=samfrac{a_{final}-a_{initial}}{2 \pi b} \
theta_{final}=frac{2 \pi (a_{final}-a_{initial})}{2 \pi b} \
theta_{final}=samfrac{a_{final}-a_{initial}{b}
hange{align*} {final=samfrac}=samfac {a_{final}-a_{initial}}{b}
heta_{final}}{final}=samfac {a_{final}-a_{initial}=samfc {b}
hange{align*}
スパイラルを0以外の角度から始めたいですか? もしそうなら、パラメータの式で最終角度にこの初期角度を加える必要がある: theta_f=happy{a_final}-a_{initial}{b}+theta_0.
既存のスパイラル曲線を二回複製して、初期のスパイラル曲線に対して-happy{thick}{2}と+happy{thick}{2}のオフセットを持つこれらの曲線はスパイラルに厚みができるように配置することが可能である。 上下のスパイラルを正しく配置するためには、オフセットされたスパイラルが初期のスパイラル曲線に垂直であることを確認する必要がある。 これは、オフセット距離୧⃛(๑⃙⃘◡̈๑⃙⃘)୨⃛にスパイラルカーブに垂直な単位ベクトルを乗じることで実現できます。 パラメトリック形式の曲線に対する法線ベクトルの方程式は次の通りである:
半厚ずれのアルキメデス螺旋に対する更新したパラメトリック方程式は次の通りである。
x_{component}=(a+bs)cos(s)-\frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}\frac{thick}{2} \
y_{component}=(a+bs)sin(s)+⃛frac{dx/ds}{sqrt{(dx/ds)^2+(dy/ds)^2}}⑯end{align*}
パラメトリック曲線の式場でこれらの方程式を書き出すことはかなり時間のかかることである。 そのため、以下の表記法を導入します:
N_x=-themefrac{dy/ds}{sqrt{(dx/ds)^2+(dy/ds)^2}} \\
N_y=\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2 }}
\end{align*}
ここで、各N_xとN_yは、最初のパラメトリックカーブのX_{fun}とY_{fun}の定義と同様に、COMSOL Multiphysicsの解析関数で定義します。 この関数では、次のスクリーンショットに示すように、微分演算子 d(f(x),x) を使用して微分を行います。
次に、関数 X_{fun}、Y_{fun}、N_x、および N_y は、片側の曲線に対するパラメトリック曲線の式で直接使用できます:
x_{lower}=X_{fun}(s)+N_x(s)♪ \frac{thick}{2} \\
y_{lower}=Y_{fun}(s)+N_y(s)\frac{thick}{2}
\end{align*}
この関数は反対側の曲線にも使えます:
x_{upper}=X_{fun}(s)-N_x(s)♪ \frac{thick}{2} \
y_{upper}=Y_{fun}(s)-N_y(s)\frac{thick}{2}
end{align*}
2つのパラメトリック曲線のうちの2番目の方程式
2曲線の端部を結合するには、上記の方程式を少し修正してパラメトリック曲線をさらに2つ追加します。 螺旋の中心を結合する曲線については、X_{fun}, Y_{fun}, N_x, N_yを角度θの開始値で評価しなければならない。 螺旋の外側に結合する曲線については、θの最終値を評価する必要がある。 したがって、中央の結合曲線は次のようになります。
X_{fun}(theta_0)+s\cdot N_x(theta_0)\cdot}{thick}{2} \\
Y_{fun}(theta_0)+s\cdot N_y(theta_0)\cdot\frac{thick}{2}
\end{align*}
一方、外側の結合曲線は次のようになる:
X_{fun}(theta_f)+s\cdot N_x(theta_f)\cdot{thick}{2} \\
Y_{fun}(theta_f)+s\cdot N_y(theta_f)\cdot\frac{thick}{2}
\end{align*}
スパイラルの一端を結合する曲線の方程式。
これで、スパイラルの中心線とプロファイルのすべての 4 つの側面を定義する 5 つの曲線が揃いました。 中心線を記述する曲線は本当に必要ではないので、無効にする(または削除する)ことができ、スパイラルのアウトラインだけが残ります。 スパイラルのアウトラインが定義されると、ソリッドに変換操作で単一のジオメトリオブジェクトを作成することができます。
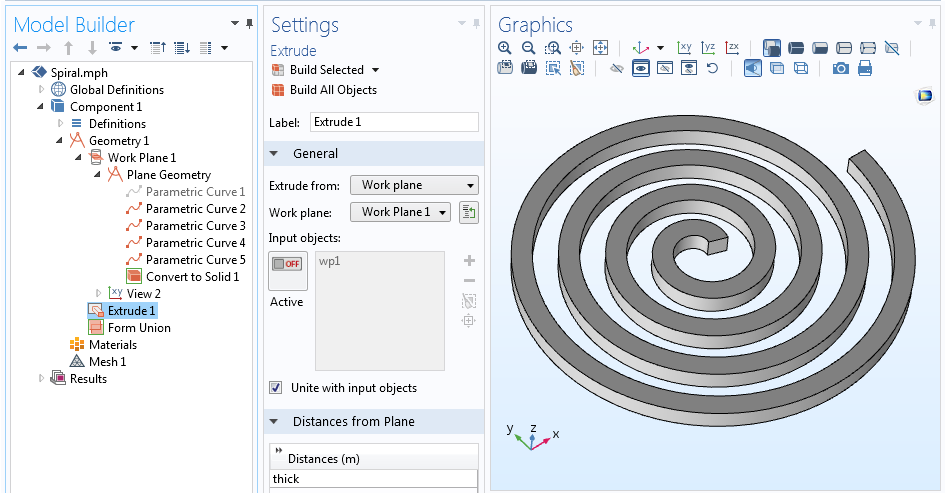
完全なジオメトリ シーケンスと押し出された 3D スパイラル ジオメトリ
COMSOL Multiphysics におけるアルキメデス螺旋のモデリングのまとめ
ここまで、完全にパラメータ化したアルキメデス螺旋を作る手順を説明しました。 この螺旋形状を使用すると、パラメータを変更してさまざまな設計を試すことができ、また、最適化調査のパラメータとして使用することもできます。 このテクニックをご自身のモデリング プロセスに活用し、特定のスパイラル ベースのエンジニアリング設計の解析を進めることをお勧めします。