Spirale archimedesowskie są często używane w analizie cewek indukcyjnych, spiralnych wymienników ciepła i urządzeń mikrofluidycznych. Dzisiaj zademonstrujemy jak zbudować spiralę Archimedesa używając równań analitycznych i ich pochodnych do zdefiniowania zestawu krzywych spiralnych. Na podstawie tych krzywych, stworzymy geometrię 2D o określonej grubości, ekstrudując ją do pełnej geometrii 3D.
Krótkie wprowadzenie do spirali Archimedesa
Skrajnie obserwowane w naturze, spirale, lub heliksy, są wykorzystywane w wielu projektach inżynierskich. Jako inżynier elektryk, na przykład, możesz nawijać cewki indukcyjne w spiralne wzory i projektować anteny spiralne. Jako inżynier mechanik, możesz używać spirali przy projektowaniu sprężyn, kół zębatych śrubowych, a nawet mechanizmu zegarkowego przedstawionego poniżej.

Przykład spirali Archimedesa używanej w mechanizmie zegarowym. Zdjęcie autorstwa Greubel Forsey. Licensed by CC BY-SA 3.0, via Wikimedia Commons.
W tym miejscu skupimy się na szczególnym rodzaju spirali, tej, która występuje w mechanizmie pokazanym powyżej: spirali Archimedesa. Spirala Archimedesa jest rodzajem spirali, która ma stałą odległość pomiędzy kolejnymi obrotami. Dzięki tej własności znajduje ona szerokie zastosowanie w projektowaniu cewek i sprężyn płaskich.
Spiralę Archimedesa możemy opisać następującym równaniem we współrzędnych biegunowych:
gdzie a i b są parametrami określającymi początkowy promień spirali oraz odległość między jej kolejnymi zwojami, przy czym ta druga wartość jest równa 2 \pi b. Zauważmy, że spirala Archimedesa bywa też nazywana spiralą arytmetyczną. Nazwa ta pochodzi od arytmetycznego postępu odległości od początku do punktu na tym samym radialu.
Designing a Parameterized Archimedean Spiral Geometry
Jak już wprowadziliśmy spirale Archimedesa, przyjrzyjmy się jak sparametryzować i stworzyć taki projekt do analizy w COMSOL Multiphysics.
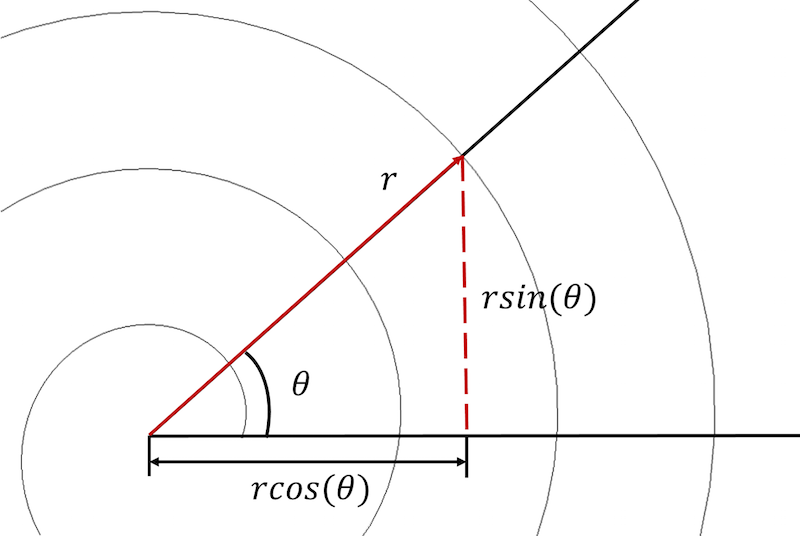
Spirala Archimedesa może być opisana zarówno we współrzędnych biegunowych jak i kartezjańskich.
Na początek musimy przekonwertować równania spirali z biegunowego na kartezjański układ współrzędnych i wyrazić każde równanie w postaci parametrycznej:
x_{component}=rcos(ąta)
y_{component}=rsin(ąta)
end{align*}
Ta transformacja pozwala nam przepisać równanie spirali Archimedesa w postaci parametrycznej w kartezjańskim układzie współrzędnych:
x_{component}=(a+b\theta)cos(\theta)
y_{component}=(a+b\theta)sin(\theta)
end{align*}
W programie COMSOL Multiphysics konieczne jest podjęcie decyzji o zestawie parametrów, które będą definiowały geometrię spirali. Parametrami tymi są: początkowy promień spirali a_{initial}, końcowy promień spirali a_{final} oraz pożądana liczba obrotów n. Szybkość wzrostu spirali b może być wyrażona jako:
Ponadto musimy zdecydować o kącie początkowym spirali theta_0 oraz kącie końcowym theta_f. Zacznijmy od wartości theta_0=0 i theta_f=2 \pi n. Mając te informacje, jesteśmy w stanie zdefiniować zestaw parametrów dla geometrii spirali.
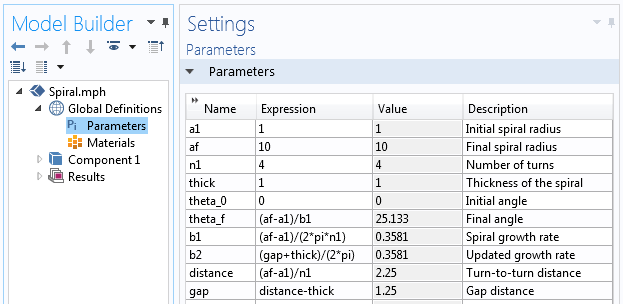
Parametry użyte do budowy geometrii spirali.
Aby zbudować tę spiralę, zaczniemy od komponentu 3D i utworzymy płaszczyznę Work Plane w gałęzi Geometry. W geometrii płaszczyzny roboczej dodamy następnie krzywą parametryczną i użyjemy równań parametrycznych, o których mowa powyżej, ze zmiennym kątem, aby narysować 2D wersję spirali Archimedesa. Równania te można wprowadzić bezpośrednio do pola Wyrażenie krzywej parametrycznej lub najpierw zdefiniować każde równanie w nowej funkcji analitycznej jako:
X_{fun}=(a+bs)cos(s) \
Y_{fun}=(a+bs)sin(s) \
end{align*}
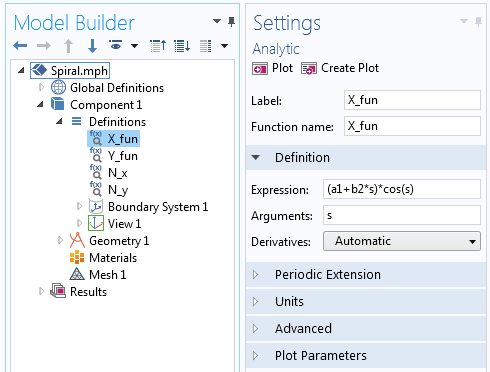
Składowa X równania spirali Archimedesa zdefiniowana w funkcji Analitycznej.
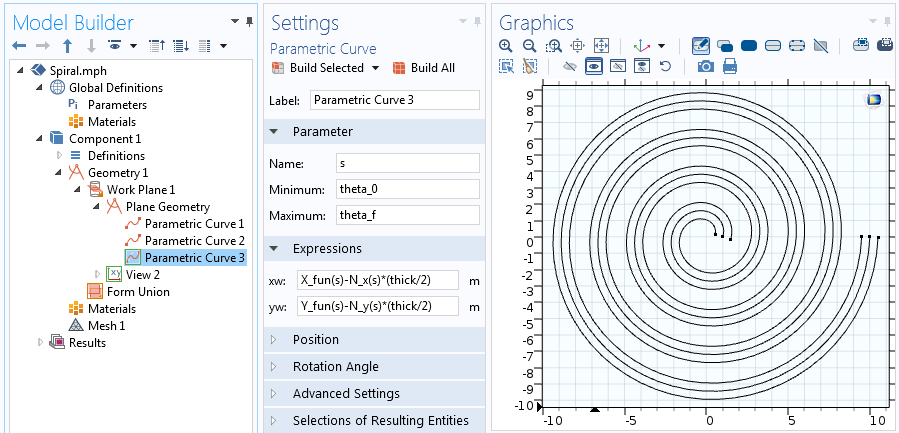
Funkcja analityczna może być użyta w wyrażeniach dla krzywej parametrycznej. W tej krzywej parametrycznej zmieniamy parametr s od kąta początkowego spirali, theta_0, do kąta końcowego spirali, theta_f=2 \pi n.
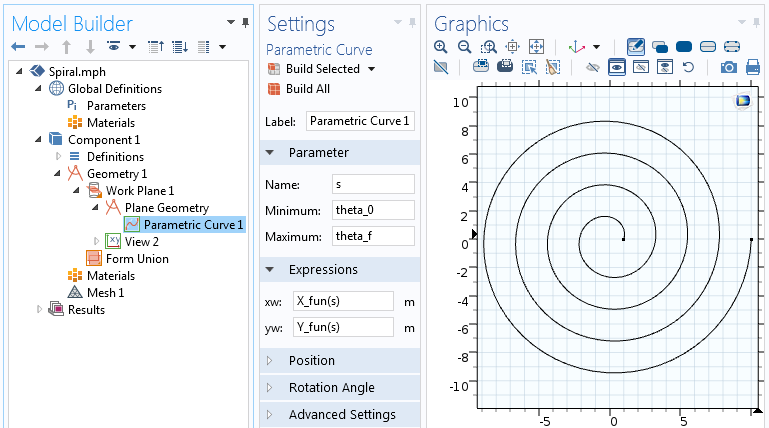
Ustawienia funkcji Krzywa parametryczna.
Równania spirali parametrycznej użyte w funkcji Krzywa parametryczna dadzą w wyniku spiralę reprezentowaną przez krzywą. Rozbudujmy teraz tę geometrię, dodając do niej grubość, aby utworzyć obiekt bryłowy 2D.
Do tej pory nasza spirala była parametryzowana pod względem promienia początkowego a_{initial}, promienia końcowego a_{final} oraz pożądanej liczby obrotów n. Teraz musimy włączyć grubość jako kolejny parametr kontrolny do równania spirali.
Zacznijmy od głównej własności spirali, która mówi, że odległość między zakrętami spirali jest równa 2 \pi b. Jest to również równoważne \frac{a_{final}-a_{initial}}{n}. Aby uwzględnić grubość, przedstawiamy odległość pomiędzy każdym kolejnym skrętem spirali jako sumę grubości spirali i pozostałej szczeliny pomiędzy skrętami, thick+gap.
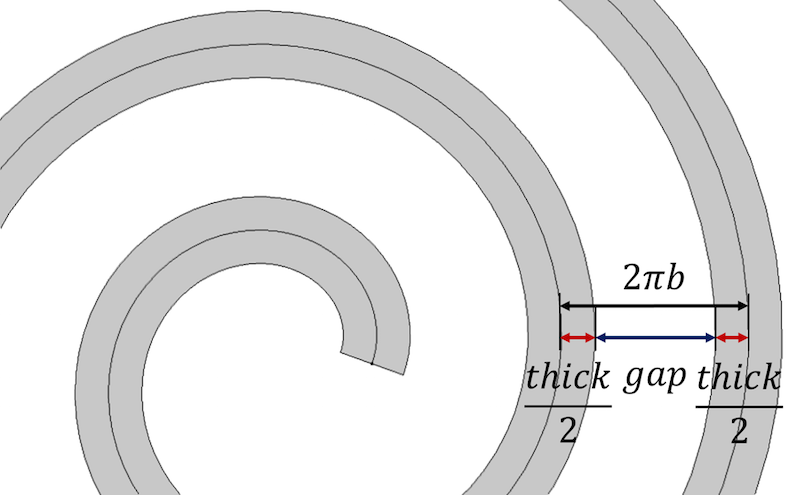
Dystans pomiędzy skrętami spirali jest zdefiniowany w kategoriach parametrów grubości spirali i szczeliny.
Aby kontrolować grubość i uzyskać identyczną odległość między zwojami, odległość można wyrazić jako:
distance=frac{a_{initial}-a_{final}}{n} \\
gap=distance-thick
\end{align*}
Po zdefiniowaniu grubości i wyrażeniu przerwy między skrętami w kategoriach grubości i stałej odległości między osiami symetrii spirali, możemy przepisać parametr wzrostu spirali w kategoriach grubości jako:
distance=2\pi b \b=frac{gap+thick}{2\pi}
end{align*}
Będziemy również chcieli wyrazić końcowy kąt spirali w terminach jej początkowych i końcowych promieni:
theta_{final}=2 \i n \i>
a_{final}=tekst{całkowita odległość}+a_{initial} \\
a_{final}=2 \i bn+a_{initial} \\
n= \frac{a_{final}-a_{initial}}{2 \pi b} \
theta_{final}= \frac{2 \pi (a_{final}-a_{initial})}{2 \pi b} \
\theta_{final}= \frac{a_{final}-a_{initial}}{b}
\end{align*}.
Chcesz rozpocząć spiralę od kąta innego niż zero? Jeśli tak, będziesz musiał dodać ten kąt początkowy do kąta końcowego w wyrażeniu na parametr: theta_f=}frac{a_{final}-a_{initial}}{b}+theta_0.
Dwukrotne powielenie istniejącej krzywej spiralnej i umieszczenie tych krzywych z przesunięciem -frac{thick}{2} i +frac{thick}{2} względem początkowej krzywej spiralnej pozwala nam zbudować spiralę o grubości. Aby prawidłowo ustawić górną i dolną spiralę, musimy upewnić się, że przesunięte spirale są normalne względem początkowej krzywej spirali. Można to osiągnąć poprzez pomnożenie odległości przesunięcia \prac{thick}{2} przez wektor jednostkowy normalny do krzywej spirali. Równania wektorów normalnych do krzywej w postaci parametrycznej są następujące:
gdzie s jest parametrem użytym w funkcji Parametric Curve. Aby otrzymać normalną jednostkową, musimy podzielić te wyrażenia przez długość normalnej:
Nasze zaktualizowane równania parametryczne dla spirali Archimedesa z przesunięciem o połowę grubości wynoszą:
x_{component}=(a+bs)cos(s)-\frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}}\frac{thick}{2} \\
y_{component}=(a+bs)sin(s)+\frac{dx/ds}{sqrt{(dx/ds)^2+(dy/ds)^2}} \frac{thick}{2}
\end{align*}
Wypisywanie tych równań w polach wyrażenia krzywej parametrycznej może być dość czasochłonne. W związku z tym wprowadzamy następującą notację:
N_x=– \frac{dy/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2}} \\
N_y=\frac{dx/ds}{\sqrt{(dx/ds)^2+(dy/ds)^2 }}
\end{align*}
gdzie każde N_x i N_y jest zdefiniowane poprzez funkcję Analytic w COMSOL Multiphysics, podobnie jak zdefiniowaliśmy X_{fun} i Y_{fun} dla pierwszej krzywej parametrycznej. W ramach funkcji używamy operatora różniczkowania, d(f(x),x), aby wykonać pochodną, jak pokazano na poniższym zrzucie ekranu.
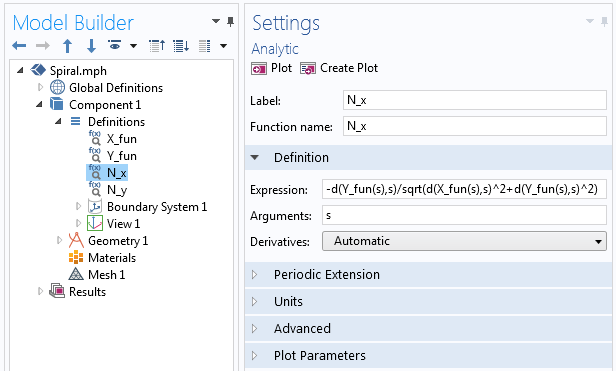
Przykłady operatora pochodnej używanego w funkcji Analytic.
Funkcje X_{fun}, Y_{fun}, N_x, oraz N_y mogą być następnie użyte bezpośrednio w wyrażeniach krzywej parametrycznej dla krzywej po jednej stronie:
x_{lower}=X_{fun}(s)+N_x(s)\frac{thick}{2}. \\
y_{lower}=Y_{fun}(s)+N_y(s)\frac{thick}{2}
\end{align*}
Funkcje te można również zastosować do krzywej po drugiej stronie:
x_{upper}=X_{fun}(s)-N_x(s)\frac{thick}{2} \\
y_{upper}=Y_{fun}(s)-N_y(s)\frac{thick}{2}
Równania dla drugiej z dwóch przesuniętych krzywych parametrycznych.
Aby połączyć końce dwóch krzywych, dodajemy dwie kolejne krzywe parametryczne, stosując niewielką modyfikację równań wymienionych powyżej. Dla krzywej, która łączy środek spirali, musimy obliczyć X_{fun}, Y_{fun}, N_x oraz N_y dla wartości początkowej kąta theta. Dla krzywej, która łączy się z zewnętrzną stroną spirali, musimy oszacować końcową wartość kąta theta. Zatem krzywa łącząca w środku ma postać:
X_{fun}(theta_0)+sdot N_x(theta_0)\frac{thick}{2} \\
Y_{fun}(theta_0)+s\cdot N_y(theta_0)\cdot\frac{thick}{2}
\end{align*}
Zewnętrzna krzywa łączenia, tymczasem, to:
X_{fun}(theta_f)+sdot N_x(theta_f)\\frac{thick}{2} \\
Y_{fun}(theta_f)+s\cdot N_y(theta_f)\cdot\frac{thick}{2}
\end{align*}
W obu powyższych równaniach s przechodzi od -1 do +1, jak pokazano na poniższym zrzucie ekranu.
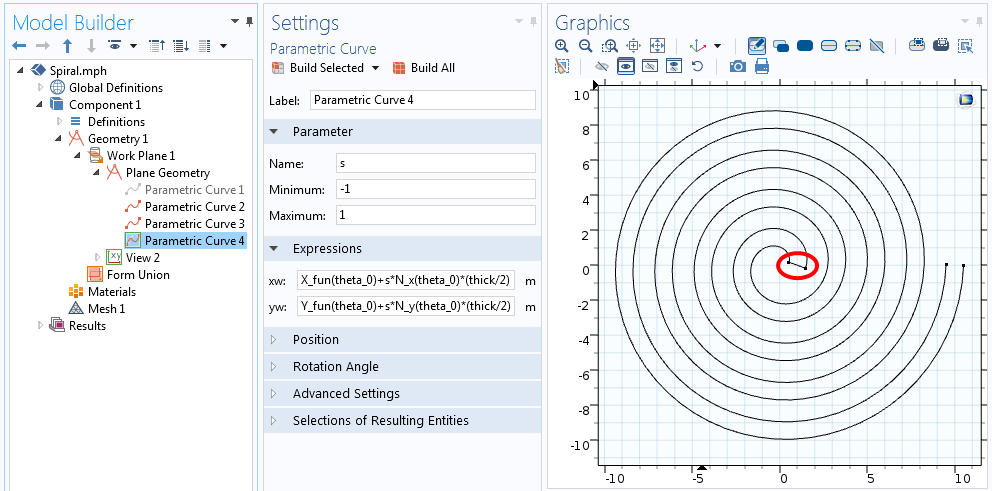
Pytania dla krzywej, która łączy jeden koniec spirali.
Mamy teraz pięć krzywych, które definiują linię środkową spirali i wszystkie cztery boki profilu. Możemy wyłączyć (lub nawet usunąć) krzywą opisującą linię środkową, ponieważ nie jest ona naprawdę potrzebna, pozostawiając tylko kontur spirali. Mając zdefiniowany kontur naszej spirali, można użyć operacji Convert to Solid (przekształć w bryłę), aby utworzyć pojedynczy obiekt geometryczny. Spirala 2D może zostać wyekstrudowana do 3D poprzez operację Extrude.
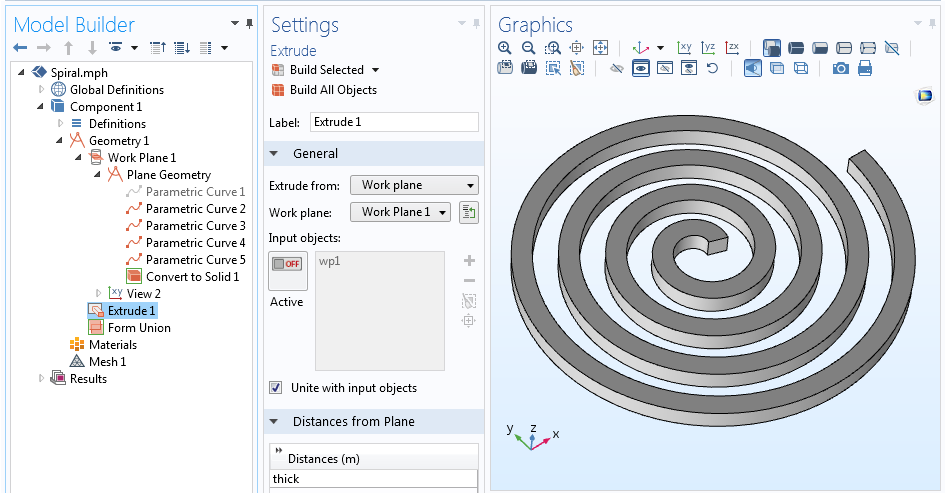
Pełna sekwencja geometrii i wyekstrudowana geometria spirali 3D.
Uwagi końcowe na temat modelowania spirali Archimedesa w COMSOL Multiphysics
Przeprowadziliśmy Cię przez etapy tworzenia w pełni parametryzowanej spirali Archimedesa. Dzięki tej geometrii spirali można zmieniać dowolne parametry i eksperymentować z różnymi projektami, a nawet używać ich jako parametrów w badaniach optymalizacyjnych. Zachęcamy do wykorzystania tej techniki w swoich własnych procesach modelowania, posuwając naprzód analizę Twojego konkretnego projektu inżynierskiego opartego na spirali.